but then I've read the definition on the forum here , that no current flows through a capacitor.
It's possible to get quite a good intuitive sense for the behavior of a capacitor by studying its basic characteristic equation, I = C\frac{dv}{dt}. This shows that current can flow through a capacitor when the rate of change of voltage with respect to time, \frac{dv}{dt} is not zero. That's one reason capacitors come in so handy, they can block a DC current and still let AC pass, for example when one needs to couple signals between two stages in an amplifier that are operating at different bias voltages.
i understand from all of your replies (which i very much appreciate, thank you all

that in the second 2nd circuit , the capacitor will charge through the diode.
my question is,
how is it possible? ,
if there is only one direction allowed. from - to + how will the capacitor charge?
Again, from the characteristic equation of the capacitor, I = C\frac{dv}{dt}, we see that the voltage across a capacitor
cannot change instantaneously. The smaller you make the rate of change of voltage across the capacitor, \frac{dv}{dt}, the larger the current becomes. The capacitor could only charge in zero time if the current were infinite, which is of course impossible. So in the second circuit, let's say you have the LED and resistor hooked up to the capacitor and apply the power. Boom, at that instant the positive end of the capacitor is at 9-LedVdrop = 7.8 volts. But because the voltage across the capacitor can't change instantaneously, that means the negative end of the capacitor at that instant is also at 7.8 volts! So if you stuck a voltmeter across the capacitor and read the voltage across the capacitor at that instant, 7.8 volts - 7.8 volts = 0 volts, the capacitor is uncharged. However, now we have the negative end of the capacitor at 7.8 volts connected to ground at zero volts. Things can't stay like that forever, two objects at different potentials interacting with each other for any length of time would violate the conservation of energy! Electrons are attracted to the positive electric field applied to the positive plate of the capacitor and move up from ground to the negative plate of the capacitor. The voltage across the capacitor begins to increase, until the capacitor is fully charged at 7.8 volts. In electronics we talk about current flowing from positive to negative, of course that's not really what's happening, but it makes it so you don't have to constantly take the square root of negative numbers when doing simple circuit analysis.
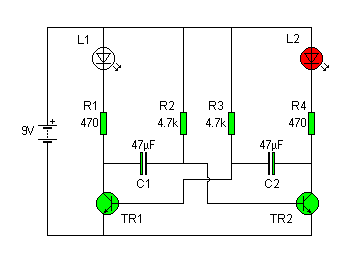
The fact that a capacitor cannot change the voltage across it instantaneously is used to good effect in the multivibrator circuit above. When the capacitor C1 is charged to 7 volts or so, and transistor TR1 turns on, its positive plate is immediately connected to 0 volts. Since the negative side was at 0 volts to begin with, that side has
no choice but to drop down to -7 volts. That large negative voltage across TR2's base-emitter junction immediately shuts TR2 down, allowing the cycle to repeat.
Here are two videos from one of MIT's undergraduate Electromagnetics courses that might help your understanding. The first discusses the way in which capacitors store charge in relation to the work-energy theorem. The second goes into the concept of capacitor dielectrics and dielectric polarization and explains why for example capacitors with certain dielectrics (like electrolytic caps) can store much more energy than one would expect based on their size. The whole lecture series itself is excellent and definitely worth watching in its entirety if you're able.
Lecture 7:
Lecture 8: