anachin6000
- 50
- 3
Homework Statement
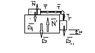
"On a horizontal table without friction it's a cube of mass M=70 kg and on the cube it's a body of mass m1=1kg. The body m1 it's conected by a cord with an other body of mass m2=4 kg, situated at hight H=1,5 m above the table. The sistem starts from 0 velocity. What it's the displacement of the cube M by the time when the body m2 touches the table(fig. 1.5.13)?(there is no friction)"
I attached the figure.
Homework Equations
T=m1*a1
T=M*a
G2-T=m2*a2 (G is weight)
a1=a2
The Attempt at a Solution
M*a=m1*a1
h=(a1*t^2)/2
d=(a*t^2)/2
h/d=a1/a=M/m1
d=h*m1/M
But at solutions in the book says d=h*m1/(m1+m2+M).
So, can someone explain me my mistake? And also I'll be very happy if someone can give me a tip for solving the problem using the momentum.