electricman
- 14
- 0
Homework Statement
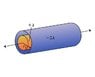
An infinitely long conducting cylindrical rod with a positive charge "lambda" per unit length is surrounded by a conducting cylindrical shell (which is also infinitely long) with a charge per unit length of "-2 lambda" and radius r1.
a) What is E(r) , the radial component of the electric field between the rod and cylindrical shell as a function of the distance r from the axis of the cylindrical rod?
Express your answer in terms of "lambda", r, and "epsilon" , the permittivity of free space.
b) What is "fi - inner" , the surface charge density (charge per unit area) on the inner surface of the conducting shell?
c) What is "fi - outer" , the surface charge density on the outside of the conducting shell? (Recall from the problem statement that the conducting shell has a total charge per unit length given by "-2 lambda" .)
d) What is the radial component of the electric field, E(r), outside the shell?
I have no idea how to solve this
Anyone that knows?