dexterdev
- 194
- 1
A doubt on statistical independence , orthogonality and uncorrelatedness ?
Hi friends,
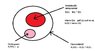
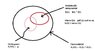
I wanted to make my concepts on statistical independence, uncorrelatedness and orthogonality clear. Suppose I have 2 random variables x and y. I have 2 pictures on the above concepts, is it correct ? which is more general picture? If any mistake is there please point it out.
What is statistical independence and linear independent independence means? Are they same?
Do pdf(x,y)=pdf(x)*pdf(y) always imply E(XY)=E(X)E(Y). Can anyone please explain that?
-Devanand T
Hi friends,
I wanted to make my concepts on statistical independence, uncorrelatedness and orthogonality clear. Suppose I have 2 random variables x and y. I have 2 pictures on the above concepts, is it correct ? which is more general picture? If any mistake is there please point it out.
What is statistical independence and linear independent independence means? Are they same?
Do pdf(x,y)=pdf(x)*pdf(y) always imply E(XY)=E(X)E(Y). Can anyone please explain that?
-Devanand T
Attachments
Last edited: