- #1
NatanijelVasic
- 19
- 5
Hi all 
Yesterday I was thinking about the central limit theorem, and in doing so, I reached a conclusion that I found surprising. It could just be that my arguments are wrong, but this was my process:
1. First, define a continuous probability distribution X.
2. Define a new random variable y = x1 + x2 + x3 + ... (Y is the sum of many independent samples of X).
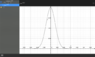
3. To visualise the distribution of Y as you sum each term, I imaging starting with the pdf of X, and convolving it with the same pdf. Then I take the result, and convolve it again with the pdf of X, and so on. According to the central limit theorem, each time you convolve the result again with the pdf of X, the new result will look more like the normal distribution, and this is the case (I have visualised this myself with graphical convolution animations).
4. It was at this point that I realized that the Fourier transform of a Gaussian is also a Gaussian.
5. I also recalled that convolution in the original domain (i.e. the operations we performed in 3) is the equivalent of multiplication in the Fourier domain.
6. As a result of points 4 and 5, that implies that the Fourier transform of pdf of X, raised to a large power, will approximate a normal distribution.
What I find surprising about this conclusion is that it is possible to create almost any pdf of your choosing, even a randomly drawn squiggle that is positive and integrates to 1, and its FT^n (where n is large) will always be approximately Gaussian. Is this correct? I am trying to find an intuitive explanation for this.
Thanks for the help!
Nat

Yesterday I was thinking about the central limit theorem, and in doing so, I reached a conclusion that I found surprising. It could just be that my arguments are wrong, but this was my process:
1. First, define a continuous probability distribution X.
2. Define a new random variable y = x1 + x2 + x3 + ... (Y is the sum of many independent samples of X).
3. To visualise the distribution of Y as you sum each term, I imaging starting with the pdf of X, and convolving it with the same pdf. Then I take the result, and convolve it again with the pdf of X, and so on. According to the central limit theorem, each time you convolve the result again with the pdf of X, the new result will look more like the normal distribution, and this is the case (I have visualised this myself with graphical convolution animations).
4. It was at this point that I realized that the Fourier transform of a Gaussian is also a Gaussian.
5. I also recalled that convolution in the original domain (i.e. the operations we performed in 3) is the equivalent of multiplication in the Fourier domain.
6. As a result of points 4 and 5, that implies that the Fourier transform of pdf of X, raised to a large power, will approximate a normal distribution.
What I find surprising about this conclusion is that it is possible to create almost any pdf of your choosing, even a randomly drawn squiggle that is positive and integrates to 1, and its FT^n (where n is large) will always be approximately Gaussian. Is this correct? I am trying to find an intuitive explanation for this.
Thanks for the help!
Nat