A perfectly inelastic collision?

1. The problem statement, all variables and given/known data

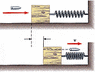
A 5.00 g bullet moving with an initial speed of 410 m/s is fired into and passes through a 1.00 kg block. The block, initially at rest on a frictionless, horizontal surface, is connected to a spring of force constant 965 N/m.

1. If the block moves 5.20 cm to the right after impact, find the speed at which the bullet emerges from the block.
wrong check mark


2. Relevant equations

p=mv (momentum)
(1/2)mv^2 (kinetic energy)
(1/2kx^2 (elastic potential energy of a spring, where x is the distance the spring is compressed)
-Energy is always conserved in a isolated system
-Momentum is always conserved in a closed isolated system

3. The attempt at a solution

I am having a hard time grappeling what type of problem this is. A perfectly inelastic collision? But the bullet then exits the block...so a little tricky. Here is my attempt:

(1/2)mv^2(initial)=(1/2)mv^2 (final) - (1/2)kx^2

solving for v (final) i got 28.4 m/s
1. The problem statement, all variables and given/known data



2. Relevant equations



3. The attempt at a solution

 

oops...already making use of my user name.

I simply forgot the word 'mechanichal'. According to my textbook, mechanical energy of a isolated system is conserved. Nonetheless, I asked my professor about the problem this morning in class, and he explained it exactly as you did, thanks! I knew conservation of momentum was involved somehow, but could not put my finger on how to apply it.

btw, thanks for the welcome! I found this site sort of as a joke using google, and to my surpise a phyics homework help does exist!

EDIT: Do you know how you could find how much mechanichal energy was transferred to internal energy?