bdvjofrni
- 2
- 0
- Homework Statement
- A wheel with six spokes is positioned perpendicular to a uniform magnetic field B of magnitude 0.5 tesla (weber per
square meter). The field is directed into the plane of the paper and is present over the entire region of the wheel as shown above.
When the switch S is closed, there is an initial current of 6 amperes between the axle and the rim, and the wheel begins to rotate.
The resistance of the spokes and the rim may be neglected.
a. What is the direction of rotation of the wheel? Explain.
b. The radius of the wheel is 0.2 meters. Calculate the initial torque on the wheel.
c. Describe qualitatively the angular velocity of the wheel as a function of time.
- Relevant Equations
- F=I*i x B
τ=r x F
This question is from 1977 AP Physics C so I suppose it would be clear enough, but I am confused about question c. Question a is easy (it rotates counterclockwise), question b too (Στ=6*rxF=6*r x (I*i x B)=0.06). Question C is where I am stuck.
The diagram provided with the question looks like this:
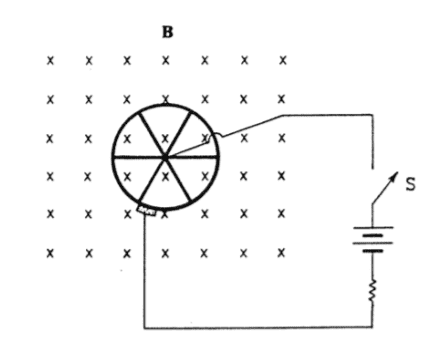
Since it is a uniform magnetic field and the area of the wheel does not change, there is no electromagnetism and the current through the wheel should be constantly 6A, which means that the total torque is always 0.06Nm. Thus, my answer is that since current does not change and ω=ω0+t*Στ/I (where I is the moment of inertia), the angular velocity will keep increasing at a constant rate Στ/I or 0.06/I.
The actual answer, however, says this:
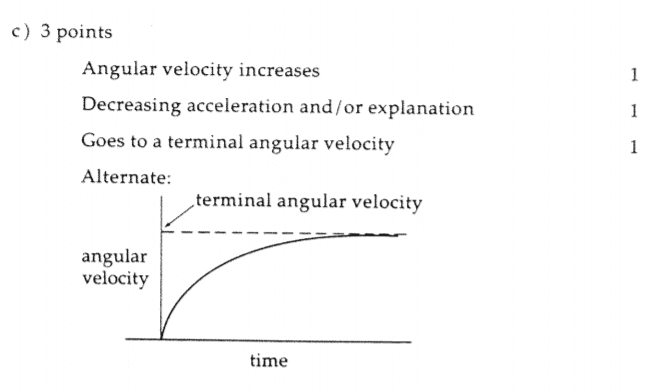
I do see why the angular acceleration will approach zero, instead of being constant. Angular acceleration approaching zero means torque approaching zero which also means current approaching zero. This seems to be the case of a RC circuit.
I'm not sure if I am understanding the diagram correctly. My understanding is that the wheel is directly connected to the circuit on both the center and the rim. I envision the connection that the rim to be some kind of brush so that the wheel can rotate, so it is physically connected to the circuit? Or does the diagram actually mean that there is a disconnect at the rim and it actually functions like a capacitor (which explains why question c's answer is this way)? Or did I miss anything else?
Thanks!
The diagram provided with the question looks like this:
Since it is a uniform magnetic field and the area of the wheel does not change, there is no electromagnetism and the current through the wheel should be constantly 6A, which means that the total torque is always 0.06Nm. Thus, my answer is that since current does not change and ω=ω0+t*Στ/I (where I is the moment of inertia), the angular velocity will keep increasing at a constant rate Στ/I or 0.06/I.
The actual answer, however, says this:
I do see why the angular acceleration will approach zero, instead of being constant. Angular acceleration approaching zero means torque approaching zero which also means current approaching zero. This seems to be the case of a RC circuit.
I'm not sure if I am understanding the diagram correctly. My understanding is that the wheel is directly connected to the circuit on both the center and the rim. I envision the connection that the rim to be some kind of brush so that the wheel can rotate, so it is physically connected to the circuit? Or does the diagram actually mean that there is a disconnect at the rim and it actually functions like a capacitor (which explains why question c's answer is this way)? Or did I miss anything else?
Thanks!