Homework Help Overview
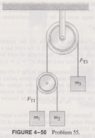
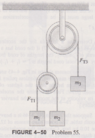
The discussion revolves around a problem involving a double Atwood machine, focusing on the dynamics of the system, including the relationships between tensions and accelerations of the masses involved. Participants are analyzing equations related to the motion of the pulleys and masses, exploring the implications of their setups and assumptions.
Discussion Character
Approaches and Questions Raised
- Some participants question the correctness of specific equations, particularly regarding the acceleration and forces acting on the masses. Others suggest alternative methods for deriving the equations of motion, including the use of Lagrangian mechanics. There is also a discussion about the effective mass and gravitational effects in the system.
Discussion Status
Participants are actively engaging with each other's ideas, providing insights and corrections regarding the equations presented. There is a recognition of the complexity of the problem, with some expressing appreciation for the Lagrangian approach while others are still grappling with the concepts. No consensus has been reached, but several productive lines of inquiry are being explored.
Contextual Notes
There are references to specific equations and assumptions that may not be fully clarified, indicating potential gaps in information or understanding among participants. The discussion also reflects the challenges of applying different mechanics frameworks to the problem.