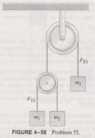
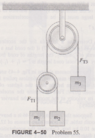
Minming said:
As an exercise, I decided to hit this with some Lagrangian mechanics:
I took ##x_1, x_2, x_3## as the (downward positive) displacements of the masses, and ##X_1, X_2## as the displacements of ##m_1, m_2## relative to the pulley over which they slide. We have the constraints:
$$x_1 = X_1 - x_3, \ x_2 = X_2 - x_3, \ X_2 = -X_1$$Which leads to$$x_2 = -x_1 -2x_3$$This leads to the Lagragian:$$L = KE - PE$$$$L = \frac 1 2 m_1 \dot x_1^2 + \frac 1 2 m_2(\dot x_1 + 2x_3)^2 + \frac 1 2 m_3\dot x_3^2 + \big (m_1x_1 - m_2(x_1 + 2x_3) + m_3x_3 \big ) g$$Then we use the Euler-Lagrange equations (##i = 1, 3##):
$$\frac{\partial L}{\partial x_i} = \frac d {dt}\frac{\partial L}{\partial \dot x_i}$$The first equation is:
$$\frac{\partial L}{\partial x_1} = \frac d {dt} \frac{\partial L}{\partial \dot x_1}$$$$\Rightarrow (m_1 - m_2)g = \frac d {dt} \bigg (m_1\dot x_1 + m_2(\dot x_1 + 2\dot x_3) \bigg )$$$$\Rightarrow (m_1 + m_2)\ddot x_1 + 2m_2 \ddot x_3 = (m_1 - m_2) g$$Similarly, the second Euler-Lagrange equation is:
$$2m_2 \ddot x_1 + (4m_2 - m_3)\ddot x_3 = (m_3 - 2m_2)g$$Eliminating ##\ddot x_1## gives:
$$(m_1m_3 + m_2m_3 + 4m_1m_2)\ddot x_3 = (m_1m_3 +m_2m_3 - 4m_1m_2)g$$Eliminating ##\ddot x_3## gives:$$(m_1m_3 + m_2m_3 + 4m_1m_2)\ddot x_1 = (4m_1m_2 + m_1m_3 - 3m_2m_3)g$$You can then get the tension from ##T_i = m_i(g - \ddot x_i)##.
The quickest way to get ##\ddot x_2## is to note that by symmetry it must be the same as ##\ddot x_1## with ##m_1## and ##m_2## interchanged.
Tough problem and not much easier using Euler-Lagrange.