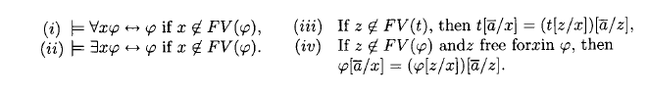A question on substitution in predicate logic

[Mathelogician]

Hi everybody!
I am confused about what is the role of the condition " xdoesn't belong to FV(phi)" in theorems like (i),(ii) or similarly in (iii) and (iv) .
I know that the philosophy of the condition "the variable z's being free for x in phi" is to avoid the phenomenon that a free variable turn to be bound after aubstituation. But i certainly don't get the point of the first type conditions!
==========================================
Any help would be thanked; the more precise one, the deeper one!
Note: FV(phi):= the set of free variables of phi ; and i am using Van Dalen's Logic and structure.

 

[Evgeny.Makarov]

The reason for the requirement in (i) and (ii) is trivial. The convention in van Dalen is that quantifiers bind more strongly than binary connectives, so (i) means \[\models (\forall x\,\varphi)\leftrightarrow\phi. \tag{*}\] Now, suppose that $x$ is the only free variable in $\varphi$. Then the left-hand side of the equivalence is a closed formula, while the right-hand side has a free $x$. Common sense says that this cannot be a law that holds for all possible $\varphi$. Strictly speaking, under the assumption above (*) may hold for some $\varphi$ because it means \[\models\forall x\, ((\forall x\, \varphi)\leftrightarrow\phi). \tag{**}\] For example, (**) holds when $\varphi$ is $x=0\lor x\ne0$. However, (**) is also false for some $\varphi$, for example, $x=0$. Formally, the condition $x\notin FV(\varphi)$ is used in the proof of (i) and (ii): under this condition, $\varphi[\bar{a}/x]$ is $\varphi$, so \begin{align*}[\![\forall x\,\varphi]\!]_{\mathfrak{A}} :&= \min\{[\![\varphi[\bar{a}/x]]\!]_{\mathfrak{A}} \mid a\in|\mathfrak{A}|\}\\ &= \min\{[\![\varphi]\!]_{\mathfrak{A}} \mid a\in|\mathfrak{A}|\\ &= [\![\varphi]\!]_{\mathfrak{A}}\end{align*}

For (iii) and (iv), I'll just give counterexamples. If $t=x+z$, then $t[0/x]=0+z$, but $t[z/x][0/z]=(z+z)[0/z]=0+0$. A similar thing happens when $\varphi$ is $x+z=0$.

P.S. I did not notice before something that looks like $\Psi$ on the Iranian flag. (Smile) I know that mathematics is done at a pretty high level in Iran.

 

[Mathelogician]

Thanks my friend Evgeny!
I think i got the point (Certainly got the Forml reason at least!) for (i) and (ii).
Though i got the counter examples for (iii) and (iv), a more in deph and formlistic explanation would be more helpful; because as i get toward in Van Dalen's paper, i see more and more uses of such conditions!And about the flag: That sign is an artistic form of the for the word "Allah-الله"(= God, originally Arabic ; and used in Islamic tradition) written in symmetric form; used after the islamic revoloution of iran instead of a "Lion-Sun" sign!

 

[Evgeny.Makarov]

Though i got the counter examples for (iii) and (iv), a more in deph and formlistic explanation would be more helpful; because as i get toward in Van Dalen's paper, i see more and more uses of such conditions!

There is nothing tricky here. I am not sure whether you need more intuition about this fact or you need a formal proof. If the former, then you just need to imagine a string of letters, including several x's, written on paper. First you replace all x's with z's and then you replace all z's with a's. The result, obviously, is the same as if you replaced all x's with a's, unless you had z's along with x's in the beginning. In that case, you would replace not only x's, but the original z's as well (during the second step, i.e., when you replaced all z's with a's).

And if you need a "more in-depth and formal explanation", as you write, then you need to look at the proofs of these properties in the book and ask questions here if necessary. In the fourth edition (2008), properties (iii) and (iv) (Corollary 2.5.5) follow from much more flexible and useful property \[(t[s/x])[r/y] = (t[r/y])[s[r/y]/x]\tag{*}\]
when $x\notin FV(r)$ (Lemma 2.5.4), which has a detailed proof. Indeed, set $s=z$ and $r=\bar{a}$; then (*) says \[t[z/x][\bar{a}/z] =t[\bar{a}/z][z[\bar{a}/z]/x] = (\text{since}\ z\notin FV(t))\ t[z[\bar{a}/z]/x] =t[\bar{a}/x].\] It does take some time to develop intuition about (*), but again it is possible by thinking about strings of letters on paper.

 

[Mathelogician]

Thanks again;
I feel better now at least about the intuition i got!