A question on velocity addition

[charlespune]

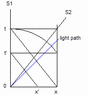
Consider frame S1 and another frame S2 moving with a velocity v with respect to S1 along +X direction. Consider a photon comes in -X direction. Velocity of photon in S1 is c.I would like to find the velocity of light in S2 from S1 without forgetting length contraction and time dilation as follows.

Observer in S1 thinks like this. For one second in his clock the clock in S2 will run $$\sqrt{1-v^{2}/c^{2}}$$ seconds. In this time the relative separation between the observer in S2 and photon decreases by (c+v)$$\sqrt{1-v^{2}/c^{2}}$$ considering length contraction.

So from S1 point of view using relativity theory the velocity of photon measured by S2 will be distance/ time = c+v. But it has to be c which we get from velocity addition rule also.

What is wrong here?

 

[jtbell]

You probably also need to take relativity of simultaneity into account. I haven't thought about your specific situation in detail yet, but in my experience, in general you need to take into account all three of (1) length contraction, (2) time dilation, and (3) relativity of simultaneity, in order to get consistent results in two reference frames.

Or use the Lorentz transformation equations. which incorporate all three effects, and from which all three effects can be derived.

 

[Doc Al]

Observer in S1 thinks like this. For one second in his clock the clock in S2 will run $$\sqrt{1-v^{2}/c^{2}}$$ seconds. In this time the relative separation between the observer in S2 and photon decreases by (c+v)$$\sqrt{1-v^{2}/c^{2}}$$ considering length contraction.

From the view of the S1 observer, the photon and observer S2 separate at the rate of c+v.

So from S1 point of view using relativity theory the velocity of photon measured by S2 will be distance/ time = c+v. But it has to be c which we get from velocity addition rule also.

No, done correctly, observer S2 will measure the speed of the photon as being c.

What is wrong here?

When taking the results according to S1 and converting them to S2 measurements, you failed to consider the relativity of simultaneity.

[jtbell beat me to it! ]

 

[JesseM]

Yes, it's all about the relativity of simultaneity, you have to take into account the idea that each observer measures the difference in time between the beginning and end of the photon's journey using a pair of clocks, one at the position where the photon started and one where it ended, with the two clocks being "synchronized" in that observer's own rest frame. Then you have to realize that two clocks which are a distance x apart and synchronized in their own frame will be out-of-sync by vx/c^2 in a frame where they are moving at speed v along the axis both of them lie on. Here's a numerical example I came up with a while ago showing how if you take into account time dilation, length contraction, and the relativity of simultaneity, you do find that both observers measure the speed of the photon as c:

Say there's a ruler that's 50 light-seconds long in its own rest frame, moving at 0.6c in my frame. In this case the relativistic gamma-factor (which determines the amount of length contraction and time dilation) is 1.25, so in my frame its length is 50/1.25 = 40 light seconds long. At the front and back of the ruler are clocks which are synchronized in the ruler's rest frame; because of the relativity of simultaneity, this means that in my frame they are out-of-sync, with the front clock's time being behind the back clock's time by vx/c^2 = (0.6c)(50 light-seconds)/c^2 = 30 seconds.

Now, when the back end of the moving ruler is lined up with the 0-light-seconds mark of my own ruler (with my own ruler at rest relative to me), I set up a light flash at that position. Let's say at this moment the clock at the back of the moving ruler reads a time of 0 seconds, and since the clock at the front is always behind it by 30 seconds in my frame, then in my frame the clock at the front must read -30 seconds at that moment. 100 seconds later in my frame, the back end will have moved (100 seconds)*(0.6c) = 60 light-seconds along my ruler, and since the ruler is 40 light-seconds long in my frame, this means the front end will be lined up with the 100-light-seconds mark on my ruler. Since 100 seconds have passed, if the light beam is moving at c in my frame it must have moved 100 light-seconds in that time, so it will also be at the 100-light-seconds mark on my ruler, just having caught up with the front end of the moving ruler.

Since 100 seconds passed in my frame, this means 100/1.25 = 80 seconds have passed on the clocks at the front and back of the moving ruler. Since the clock at the back read 0 seconds when the flash was set off, it now reads 80 seconds; and since the clock at the front read -30 seconds, it now reads 50 seconds. And remember, the ruler was 50 light-seconds long in its own rest frame! So in its frame, where the clock at the front is synchronized with the clock at the back, the light flash was set off at the back when the clock there read 0 seconds, and the light beam passed the clock at the front when its time read 50 seconds, so since the ruler is 50-light-seconds long, the beam must have been moving at 50 light-seconds/50 seconds = c as well! So you can see that everything works out--if I measure distances and times with rulers and clocks at rest in my frame, I conclude the light beam moved at 1 c, and if a moving observer measures distance and times with rulers and clocks at rest in his frame, he also concludes the same light beam moved at 1 c.

If you want to also consider what happens if, after reaching the front end of the moving ruler at 100 seconds in my frame, the light then bounces back towards the back in the opposite direction towards the back end, then at 125 seconds in my frame the light will be at a position of 75 light-seconds on my ruler, and the back end of the moving ruler will be at that position as well. Since 125 seconds have passed in my frame, 125/1.25 = 100 seconds will have passed on the clock at the back of the moving ruler. Now remember that on the clock at the front read 50 seconds when the light reached it, and the ruler is 50 light-seconds long in its own rest frame, so an observer on the moving ruler will have measured the light to take an additional 50 seconds to travel the 50 light-seconds from front end to back end.

 

[jtbell]

Aha, I see JesseM got his version in while I was writing mine off-line. Here's mine, anyway:

To make calculations simpler, I measure time in seconds, distance in light-seconds (ls), and speed in ls/sec. In these units, c = 1 ls/sec.

As a "supporting prop", imagine a rod with length L = 10 ls. It is stationary in frame S1, with the left end at x = 0 and the right end at x = 10 ls. It has clocks fastened to its ends, which are synchronized in S1. A light pulse leaves the left end when both clocks read t = 0, and passes the right end when both clocks read t = 10 sec (in S1).

Frame S2 moves to the right at v = 0.8 ls/sec, relative to S1. In this frame, the rod moves to the left at that speed. Because of length contraction, the rod's length is:

$$L^{\prime} = L \sqrt {1 - v^2 / c^2} = 10 \sqrt {1 - 0.8^2} = 6$$

Because of relativity of simultaneity, the two clocks are not synchronized in S2. Their readings differ by the amount

$$\frac {v L} {c^2} = (0.8)(10) = 8$$

sec, with the right-hand clock reading "ahead" of the left-hand clock by this amount. (If the rod were moving to the left, the left-hand clock would be ahead, instead.) Both of these moving clocks "tick" at the same rate (so the difference remains constant), but slower than a stationary clock (in S2).

The light pulse leaves the left end of the rod, going towards the right, when the left-hand clock reads 0 and the right-hand clock reads 8 sec. Let's set the time in S2 so that it's also zero at this moment (t' = 0).

Does the light pulse travel the rod's contracted length L' = 6 ls before it reaches the right end? No, because the right end of the rod is moving to the left! The pulse meets the right end of the rod somewhere between x' = 0 and x' = 6 ls. Let's just call it x', an unknown quantity.

If we know the time t' in S2 when the pulse meets the right end of the rod, we can calculate x' from the initial position of the right end and its speed:

$$x^{\prime} = 6 - 0.8 t^{\prime}$$

But what is t'? It's also unknown, so far.

We do know that when the pulse meets the right end of the rod, the right-hand clock has to read 10 sec. Therefore, during the pulse's flight, 10 - 8 = 2 sec elapse on the (moving) clocks. The time dilation equation gives us the elapsed time on a stationary clock in S2:

$$\Delta t^{\prime} = \frac {\Delta t} {\sqrt{1 - v^2 / c^2}} = \frac {2} {\sqrt{1 - 0.8^2}} = 3.333$$

Therefore the pulse meets the right end of the rod at t' = 3.333 sec, which gives us x' = 6 - (0.8)(3.333) = 3.333.

Now we can calculate the speed of the light pulse in S2 as

$$c^{\prime} = \frac {x^{\prime}} {t^{\prime}} = \frac {3.333} {3.333} = 1 = c$$

This shows that we need all three of length contraction, time dilation, and relativity of simultaneity, in order to make things come out consistently (here, to make the speed of light come out to c = 1 in both frames).

 

[charlespune]

Thanks a lot. I thought relativity of simultaneity was incooperated in length contraction and time dilation.

 

[phyti]

Or simplify:
The drawing shows the perspective of S2 superposed on S1, with a common event at 0, the left end of the rod. The arc is a geometric means to determine the ratio of t' to t, the prime denoting the moving observer S2. The value t is the S1 time for S2 to travel the length of the rod. It's visually easy to see that the geometry of the S2 frame is 1/g times the S1 frame. For this and similar examples, calculate for the rest frame, then apply the time dilation factor.
v = .8 (c=1), u is the time for light to travel the length of the moving rod.
for S1: x = 10, u = x/(c+v) = 10/1.8 = 5.56 sec
for S2: u' = u/g = 3.33 sec
You are not actually calculating the speed of light, since it's already in the equations you are using. If you calculate distance as c*time, it's a sure thing. SR is formulated to preserve the constant c.