A simple area calculation, where is the mistake ?

[Yankel]

Hello all

I have solved a problem, and my answer differ from the one in the book from where it's taken. I think I did it correctly, can you assist ?

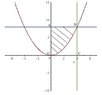
In the attached photo we have the graph of f(x)=0.5x^2
(half of x squared)

In the rectangle ABCO, BC is twice the size of OC. Calculate the dashed area.

View attachment 1186

The answer in the book is 21.3333
My answer is 10.666667

I think that 21.3333 is the area that complete to the whole rectangle. Am I right ?

Thanks !

 

[MarkFL]

Your textbook is correct. Are you given a formula, or are you supposed to use integration? I ask because you posted in the Pre-Calculus forum, so I didn't know exactly what pre-calculus technique would be used.

 

[Yankel]

Integration.

How can the area be 21.333 ?

 

[MarkFL]

Integration.

How can the area be 21.333 ?

What definite integral did you use to represent the area?

 

[M R]

Integration.

How can the area be 21.333 ?

Doesn't it look like about 2/3 of the area of rectangle ABCO.

Well, it turns out that it is exactly 2/3 of that area.

 

[MarkFL]

Doesn't it look like about 2/3 of the area of rectangle ABCO.

Well, it turns out that it is exactly 2/3 of that area.

Interestingly, it turns out to be 2/3 of the rectangular area for any parabola of the form $y=ax^2$ and for any rectangle having the opposing vertices $(0,0)$ and $\left(b,ab^2 \right)$. :D

 

[M R]

Interestingly, it turns out to be 2/3 of the rectangular area for any parabola of the form $y=ax^2$ and for and rectangle having the opposing vertices $(0,0)$ and $\left(b,ab^2 \right)$. :D

It's more general than that. It'2 2/3 for every parabola.View attachment 1187

 

[Yankel]

I used:

\[\int_{0}^{4}\frac{1}{2}x^{2}dx\]

to do the area under the function, in the normal way, I got 21.333
and then I subtracted is from 32, the area of the rectangle.

Edit: Found my mistake, stupid one actually. My way was perfect, I "forgot" to multiply by 0.5...and got opposite result.

Sorry guys

 

[MarkFL]

To find the area directly, you could use:

$$A=\int_0^4 8-\frac{x^2}{2}\,dx$$

which as you can see is equivalent to what you did. :D