A simple pulley two mass system

[Sho Kano]

In a simple one pulley-two mass system I have two ways of solving for acceleration, but am not sure which one is the correct or proper way.

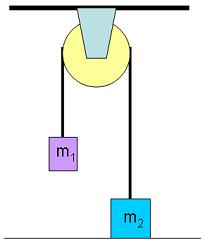
#1)
assume m2 has the greater mass of the two
T-m1g = m1a
m2g - T = m2a
a = (m2g - m1g) / (m1+m2)

#2)
direction of up is positive, down is negative
T-m1g = m1a
T-m2g = m2a
a = (m1g - m2g) / (m2-m1)

The two accelerations are different. Which one is correct, and why?

 

[BvU]

The rope has a fixed length. If m₁ goes up, m₂ goes down with the same speed. So $v_1 = -v_2$ and thereby $a_1 = -a_2$ . You only use one a in your second set. Apart from that, the second set is more clear (more consistent in signs of T and mg)

 

[Sho Kano]

The rope has a fixed length. If m₁ goes up, m₂ goes down with the same speed. So $v_1 = -v_2$ and thereby $a_1 = -a_2$ . You only use one a in your second set. Apart from that, the second set is more clear (more consistent in signs of T and mg)

Accelerations are equal to zero when summed up,
m1 is moving up at a1
m2 is moving up at -a2

a1 + -a2 = 0
a1 = a2

 

[BvU]

Accelerations are equal to zero when summed up

Yes. A consequence of $$y_1+y_2={\rm \ constant} \Rightarrow v_1+v_2= 0 \Rightarrow a_1+a_2= 0 $$
It is not wise to avoid negative numbers by redefining/assuming directions. Much better to keep one coordinate system definition and conclude directions from the signs of the calculated variables.

 

[Sho Kano]

Yes. A consequence of $$y_1+y_2={\rm \ constant} \Rightarrow v_1+v_2= 0 \Rightarrow a_1+a_2= 0 $$
It is not wise to avoid negative numbers by redefining/assuming directions. Much better to keep one coordinate system definition and conclude directions from the signs of the calculated variables.

I'm confused as to whether the second set is correct or not. Can you check the other part of post #3?

 

[EddiePhys]

#1 would work fine. If the acceleration came negative, then you know that your assumption that m2>m1 is wrong, and it would accelerate with -a in the direction opposite to what you assumed
#2 is incorrect.

 

[hackhard]

#1)
assume m2 has the greater mass of the two
T-m1g = m1a
m2g - T = m2a
a = (m2g - m1g) / (m1+m2)

this is correct!

#2)
direction of up is positive, down is negative
T-m1g = m1a
T-m2g = m2a
a = (m1g - m2g) / (m2-m1)

this is wrong
specifically the equation

T-m2g = m2a

is wrong because 'a' denotes mag of acceleration of m2 and mag of a vector is always positive
since you already know that m2 has accln downwards , so it is known that m2g must be greater than T
so since right side of eqn is +ve , so left side must also be +ve , so it must be (m2g-T) (since m2g > T)
it is always better to use vectors
T*j + mg*(-j)= m2a* (-j) j is unit vector in upward dir

 

[Sho Kano]

It all seems obvious now. These should be the equations paired with the second set.
$T\quad -\quad { m }_{ 1 }g\quad =\quad { m }_{ 1 }{ a }_{ 1 }\\ T\quad -\quad { m }_{ 2 }g\quad =\quad { m }_{ 2 }{ a }_{ 2 }\\ { a }_{ 2 }\quad =\quad { -a }_{ 1 }\\ \\ { a }_{ 1 }\quad =\quad \frac { { m }_{ 2 }g\quad -\quad { m }_{ 1 }g }{ { m }_{ 1 }\quad +\quad { m }_{ 2 } }$
Which gives the correct answer! Thanks guys.