- 1,191
- 683
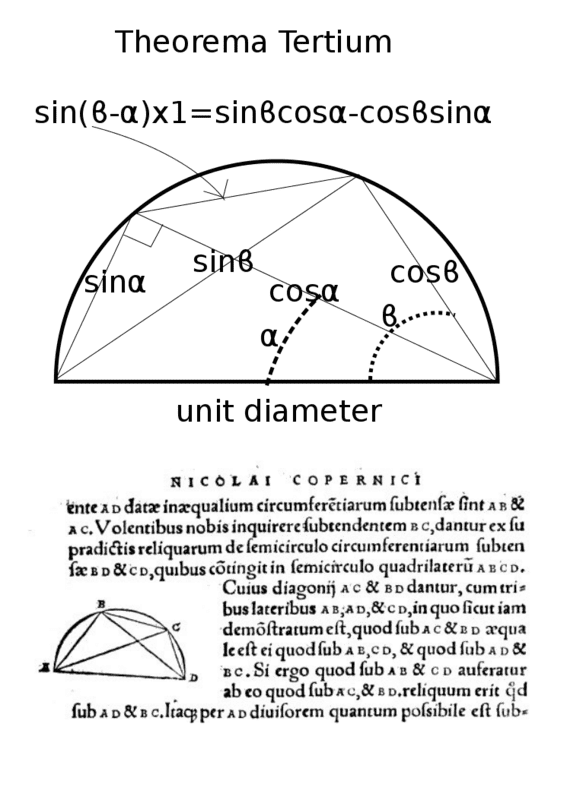
Thought following might be of interest - application of Ptolemy's Theorem from "De Revolutionibus Orbium Coelestium: Liber Primus".
Last edited by a moderator:
1. Construct a unit diameter from either end of the chord. Complete right triangle by joining end of diameter to other end of chord.dextercioby said:Amazing visual proof of the trigonometric identity, but 2 things are not clear to me.
1. Why is the upper chord ##\sin(\beta-\alpha)##?
2. What would a purely geometrical (i.e. trigonometry-free) proof of the equality "chord times diameter equals diagonals' product minus the product of the other chords" be?