Zero
- 17
- 4
- Homework Statement
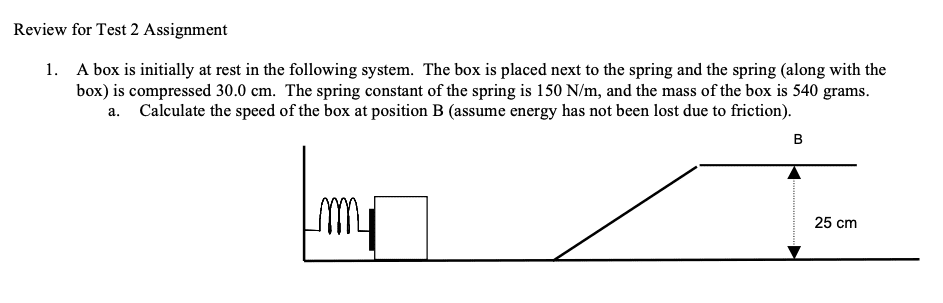
- A box is initially at rest in the following system. The box is placed next to the spring and the spring (along with the box) is compressed 30.0 cm. The spring constant of the spring is 150 N/m, and the mass of the box is 540 grams.
a. Calculate the speed of the box at position B (assume energy has not been lost due to friction).
- Relevant Equations
- Since I know energy is lost due to friction would I use the formula ff= U (Fn) where Fn= 5.292 since that would be the gravity action on the object and normal for and gravity have to be equal. If I use the same logic would Ff= -Ek or no???
f= kx
= 150 n/m (.3m)
= 45n
Ug= 1/2 kx^2
= 1/2 (150) (.3)^2
= 75 (.09)
= 6.75 j
Ek= 1/2mv^2
6.75= 1/2 (.54) (v^2)
6.75= .27 (v^2)
25= v^2
5= v1
= 150 n/m (.3m)
= 45n
Ug= 1/2 kx^2
= 1/2 (150) (.3)^2
= 75 (.09)
= 6.75 j
Ek= 1/2mv^2
6.75= 1/2 (.54) (v^2)
6.75= .27 (v^2)
25= v^2
5= v1