A thought experiment on relativistic Electrostatics

[vinven7]

Here is a thought experiment on Special Relativity involving charges which are rest with respect to each other.

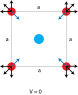
Consider a configuration of charges as shown in the image. Four identical charges (q) are placed at the corners of a square with an opposite charge at the centre (Q). The value of Q is such that the whole configuration is stable and no charge experiences a net force.
It can be shown that for this to work

[Q]/[q]= 1+\sqrt{2^{3}}

Now consider the same configuration of charges in an inertial frame of reference moving at a velocity v relative to a stationary observer. This observer should find the square to be squeezed into a rectangle as the length in the direction of motion will contract.
It should be assumed that the charges would still not experience a net force - as an observer in the same frame of reference as the charge system will not find the charges to be moving.
If the stationary observer calculates the equilibrium of the charges, he should find a new ratio for the charges:

[Q]/[q]= 1+ \sqrt{(1+\gamma^{2})^{3}}

where
\gamma = \sqrt{ 1- \frac{v^{2}}{c^{2}}}

Thus, the observer moving along with the charges will find one ratio for the charges while the observer at rest will observe another ratio.
But how can this be since they are the same system of charges and charge is itself an invariant under relativity?
I hope I have been clear enough. Please ask me if you'd like something cleared.

 

[bcrowell]

The value of Q is such that the whole configuration is stable and no charge experiences a net force.

I don't think this is right. It's not possible to have a stable, static equilibrium for a classical system of point charges. This follows from Gauss's law. I think the system you're talking about is in an unstable equilibrium.

But how can this be since they are the same system of charges and charge is itself an invariant under relativity?

You have to take into account the magnetic forces that occur in the new frame.

 

[vinven7]

I don't think this is right. It's not possible to have a stable, static equilibrium for a classical system of point charges. This follows from Gauss's law. I think the system you're talking about is in an unstable equilibrium.

Yes, they are in unstable equilibrium. I was only implying that no charge experiences a net force.


You have to take into account the magnetic forces that occur in the new frame.

In the new frame, the charges themselves are at rest relative to each other. So then why would they experience a magnetic force?
The stationary observer will however find a moving charge and will detect a magnetic field because of it - but I am not sure how the individual charges if/how respond to it.

 

[Bill_K]

In the new frame, the charges themselves are at rest relative to each other. So then why would they experience a magnetic force?

Because in the new frame they are both moving. A moving charge is equivalent to a current. A current produces a B field that wraps around the current (right hand rule) and is transverse to the direction of motion. The other moving charge experiences a Lorentz force from this B field, F = qv x B. The result is an additional attraction between the charges.