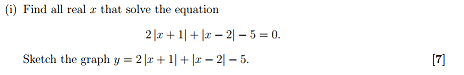stuart4512
- 3
- 0
How do I do this? I have tried a few methods and end up getting x values that don't work when placed back into the equation.
View attachment 3670
View attachment 3670