Abstract Algebra - Isomorphism

[jz0101]

1. Show that S₄₂ contains multiple subgroups that are isomorphic to S₄₁.
Choose one such subgroup H and find σ₁,...,σ₄₂ such that

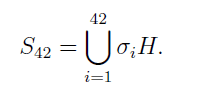
How can you solve this?? I am confused if anyone can help me to solve this!

 

[haruspex]

What, in words, does S₄₂ represent?

 

[kduna]

I'll assume you already identified a subgroup $H$ that is isomorphic to $S_{41}$. Think about the cosets of $H$. How many are there? (If this is a hard question, try looking over a proof of Lagrange's Theorem).

 

[jz0101]

@kduna: I am studying by myself reading book. Now I saw this question which I wanted to know how to solve this question.