AC circuits - some questions

[R A V E N]

Homework Statement

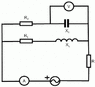
In circuit given in attachment,find the value which is showed on ammeter A,if voltmeter is showing $$50\;V$$.

Values are $$R=R_2=X_L=X_C=10\;\Omega$$ and $$R_1=5\;\Omega$$.

The Attempt at a Solution

First I calculate current thought branch with $$R_2$$ and $$X_C$$:

$$\underline{I}_2=\frac{\underline{U}}{-jX_C}=j5\;A$$

then knowing that potential difference at the ends of branches(one with $$R_2$$ and
$$X_C$$ and the other with $$R_1$$ and $$X_L$$) is the same,I proceed:

$$\underline{U}_1=\underline{U}_2$$

$$\frac{\underline{I}_1}{R_1+jX_L}=\frac{\underline{I}_2}{R_2-jX_C}$$

$$\underline{I}_1=\frac{R_1+jX_L}{R_2-jX_C}\underline{I}_2=(-3.75-j1.25)\;A$$

Overall current $$\underline{I}$$ in circuit is the sum of two currents from two branches,so:

$$\underline{I}=\underline{I_1}+\underline{I_2}=(-3.75+j3.75)\;A$$

Module of this value is value showed on ammeter:

$$|\underline{I}|=5.303\;A$$

However,correct solution is:

$$3\sqrt{5}\;A\approx6.708\;A$$

Where is the mistake?

 

[R A V E N]

The second question is a theoretical one.Suppose that we have a simple system like one illustrated in attachment.

If we need to find complex admittance of that system,we can write:

$$\underline{Y}=G+jB=\frac{1}{\underline{Z}}=\frac{1}{R+jX_L}\cdot\frac{R-jX_L}{R-jX_L}=\frac{R-jX_L}{R^2+X_L^2}=\frac{R}{R^2+X_L^2}+j\frac{-X_L}{R^2+X_L^2}$$

from where we can see that it is $$B=\frac{-X_L}{R^2+X_L^2}$$,althought it is $$B=\frac{X_L}{R^2+X_L^2}$$.

Why is this "-" just neglected,what is physical explanation of that?

Or it is just hardcore mathematical laws against imperfect physical reality?

 

[R A V E N]

OK,I managed to resolve first problem,but what about second one?

 

[R A V E N]

Probably the explanation is that while one physical parameter is rising(susceptance $$B$$),the other is lowering(inductive reactance $$X_L$$) and vice-versa,like it is in Faraday`s law of induction:

$$e=-\frac{d\phi}{dt}$$

the magnetic field which is produced by induced current(which is in turn produced by induced electromotive force $$e$$) is in oposition with the change of outer flux $$\phi$$(sorry if my technical english sounds a bit clumsy).

But what if there is capacitor instead of inductor?
In that case there is no confusion like this.