Current phase angle difference (AC circuit)

[gruba]

Homework Statement

[itex][/itex]
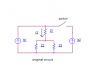
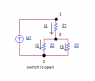
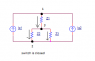
Three receivers, with complex impedance $\underline{Z_1}=(125+j375)\Omega,\underline{Z_2}=(700+j100)\Omega,\underline{Z_3}=(500-j500)\Omega$, and two sinusoidal current generators of effective values $I_{g2}=40mA$ and unknown $I_{g1}$ are connected. When the switch is open, apparent power of receiver $\underline{Z_2}$ is $S_2=\frac{\sqrt 2}{2}VA$. After the switch is closed, active power of all three receivers is reduced two times.

Find phase angle difference between $\underline{I_{g1}}$ and $\underline{I_{g2}}$

Homework Equations

Apparent power: $S=UI[VA]$
Active power: $P=S\cos\phi [W]$ where $\phi$ is the phase angle between current and voltage.
Reactive power: $Q=S\sin\phi[var]$
$P=S\cos\phi=\mathfrak{R}(\underline{S})=\mathfrak{R}(\underline{U}\cdot\underline{I^{*}})$ where $\underline{S}$ is the complex apparent power.
Current phase angle is given by $\psi=\theta-\phi$ where $\theta$ is voltage phase angle.

The Attempt at a Solution

From the impedances, we can find the phase angles $\phi_1,\phi_2,\phi_3$.
$\phi_1=\tan^{-1}\frac{375}{125}=\tan^{-1}(3)\approx 71.565^{o}$
$\phi_2=\tan^{-1}\frac{100}{700}=\tan^{-1}(1/7)\approx 8.138^{o}$
$\phi_3=\tan^{-1}\frac{-500}{500}=\tan^{-1}(-1)=-45^{o}$

When the switch is opened, we know $S_2$, and the active power of $\underline{Z_2}$ is then $P_2=S_2\cos\phi_2\approx 0.699W$.
Reactive power is $Q_2=S_2\sin\phi_2\approx 0.099 var$
Complex apparent power of $\underline{Z_2}$ is now $\underline{S_2}=(0.699+j0.099)VA$.
But, because $I_{g1}$ is unknown, from $S_2=U_{23}I_2$ we can't find $U_{23}$ and $I_2$.
Question: How to find $\underline{I_{g1}},\underline{U_{23}},\underline{I_2}$ when the switch is opened?

When the switch is closed, we have ${P_2}^{c}=\frac{{P_2}^{o}}{2}\approx 0.349W$.
But, from the first case we need $\underline{I_{g1}}$.

When we know $\underline{I_{g1}},\underline{I_{g2}}$, then we will know the phase angles $\psi_1,\psi_2$, and the phase difference is $|\psi_1-\psi_2|$.

Question: How to find $\underline{I_{g1}}$ and $\underline{I_{g2}}$?

 

[NascentOxygen]

After the switch is closed, active power of all three receivers is reduced two times.

Is this saying that over-all total active power is halved?

 

[gruba]

Is this saying that over-all total active power is halved?

Yes, the total active power is halved.

 

[gneill]

A suggestion: I think it would be helpful to start by finding the magnitude of Ig1: Assume for now that Ig1 provides the reference angle (so its phase angle is taken to be zero). Then the current through Z2 in terms of Ig1 can be found by current division. You know the impedances Z1 through Z3 so the current division amounts to a complex constant multiplied by Ig1.

Then you should be able to write an expression for the complex power for Z2. In polar form its magnitude should be the apparent power.

 

[gruba]

A suggestion: I think it would be helpful to start by finding the magnitude of Ig1

I don't know how to find the magnitude of $I_{g1}$.
What case to look for finding it (switch closed or open)?

 

[gneill]

I don't know how to find the magnitude of $I_{g1}$.
What case to look for finding it (switch closed or open)?

Switch open.

If Z2 were all alone with a current source $I$, what would be the magnitude of $I$ that would produce the given apparent power?

Now, using the current division rule, what would be the corresponding magnitude of Ig1 to produce that magnitude of current $I$?

 

[gruba]

Switch open.

If Z2 were all alone with a current source $I$, what would be the magnitude of $I$ that would produce the given apparent power?

$$S_2=U_2I=|\underline{Z_2}|^2I\Rightarrow I=\frac{\sqrt 2}{10^6}A$$

 

[gneill]

The magnitude of Z2 is 500√2 Ohms ( |700 + j100| ). Working with magnitudes: $p = I^2 Z$. You're given that p = √2/2. So what's $I$?

 

[gruba]

The magnitude of Z2 is 500√2 Ohms ( |700 + j100| ). Working with magnitudes: $p = I^2 Z$. You're given that p = √2/2. So what's $I$?

$I=1mA$
I made a mistake in squaring Z2 and not I.

 

[gneill]

Try again! (I think you may have tripped up taking the square root):

$I^2 Z =p$

$I^2 (500 \sqrt{2}) = \frac{\sqrt{2}}{2}$

$I^2 = ?$

 

[gruba]

$I\approx 0.032A$

 

[gneill]

$I\approx 0.032A$

Yup. Or 31.62 mA, or sticking with exact figures:

$I = \frac{\sqrt{10}}{100} A$

Now, what can you make of the ratio of that current magnitude to that of Ig1? Current division rule comes in handy here.

 

[gruba]

Now, what can you make of the ratio of that current magnitude to that of Ig1? Current division rule comes in handy here.

$$I_{g1}=I\cdot \frac{Z_2+Z_3}{Z_3}=\frac{\sqrt{10}}{50}A$$

Is this right?

 

[gneill]

No. Can you show more details of your calculation?

$I⋅\left| \frac{Z_2 + Z_3}{Z_3} \right| = ?$

 

[gruba]

No. Can you show more details of your calculation?

$I⋅\left| \frac{Z_2 + Z_3}{Z_3} \right| = ?$

After correction, $I_{g1}=\frac{\sqrt 2}{25}A$

 

[gneill]

Okay! That looks much better.

Now you need to consider what phase angle you need to apply to that current so that the active power in the circuit drops by half when you add in the 40 mA of Ig2. (I'm assuming that we now switch our reference angle to be that of Ig2 since it was specified to be exactly 40 mA, no imaginary part or angle). By how much do you have to scale current in order to halve the power?

 

[gruba]

Okay! That looks much better.

Now you need to consider what phase angle you need to apply to that current so that the active power in the circuit drops by half when you add in the 40 mA of Ig2. (I'm assuming that we now switch our reference angle to be that of Ig2 since it was specified to be exactly 40 mA, no imaginary part or angle). By how much do you have to scale current in order to halve the power?

Now I am really stuck...

Since we know Ig1, from the first case (switch is opened) we can evaluate all three active powers of receivers,
$$P_1\approx 0.375W, P_2\approx 0.408W,P_3\approx 0.064W,P_{total}\approx 0.847W$$

Now, we look at the second case (switch closed).
We know that now $P_{total}\approx 0.4235W$.

How to set the equations in order to find phase angle $\psi_{I_{g1}}$?
What method to use?

 

[gneill]

Just take a system-wide view of things. If some current with magnitude $I_o$ produces some power $P_o$ (and we don't really care what the particular values are at the moment), then what should current $I_1$ be so that the power is half of $P_o$? Hint: How does power vary with current (when the impedance is constant)?

 

[gruba]

Just take a system-wide view of things. If some current with magnitude $I_o$ produces some power $P_o$ (and we don't really care what the particular values are at the moment), then what should current $I_1$ be so that the power is half of $P_o$? Hint: How does power vary with current (when the impedance is constant)?

Square of current is halved when the power is halved.
But what it means in complex domain?

 

[gneill]

Square of current is halved when the power is halved.
But what it means in complex domain?

I presume that you have been introduced to the power triangle? Apparent power on the hypotenuse, real (active) power on the adjacent side, and imaginary (reactive) power on the opposite side?

The angle $\phi$ is tied to the impedance of the circuit, and thus the power factor. So long as the impedance is constant then the power triangle will have the same angle. If you manipulate the current to change the power, the triangle remains the same shape and just changes size. That is, if you change the magnitude of the current to change the power in the circuit then you just scale the triangle in size, producing a similar triangle (in the geometric sense of the work "similar").

So when you are asked to halve the active power by changing the current, know that in the complex domain real, reactive, and apparent powers will all scale by the same amount.

Now, in this problem you've already done the following:
1. Found the magnitude of the current required to produce the given apparent power in impedance Z2.
2. Found the magnitude of the current Ig1 that produces that current in impedance Z2: $I_{g1} = \frac{\sqrt{2}}{25} A$.
3. Determined how to scale a current in order to halve the power in a circuit.

What remains is to state what the magnitude of the new half-power-current should be, and associate a phase angle with your Ig1 such that when 40 mA ∠ 0 is added to Ig1 the result is a current magnitude that matches the half-power current.

Let's start with the current magnitude. With the switch open the total current is $I_{g1} = \frac{\sqrt{2}}{25} A$. Taking that as the "full power" current, what magnitude of total current will halve that power?

 

[gruba]

Taking that as the "full power" current, what magnitude of total current will halve that power?

The magnitude of total current ${I_{g1}}'=\frac{1}{5\sqrt 2}A$ will halve the power.

 

[gneill]

Can you show how you arrived at that value?

 

[gruba]

Can you show how you arrived at that value?

Let $I_{g1}=\frac{\sqrt 2}{25}A$, then ${I_{g1}}^2=\frac{2}{625}A$ (note the error in previous post).
Let ${{I_{g1}}'}^2={{I_{g1}}}^2\cdot \frac{1}{2}=\frac{1}{625}A$

Then, ${{I_{g1}}'}=\frac{1}{25}A$.

 

[gneill]

Ah. That's better

So that will be the magnitude of the current that you get when you sum Ig1 and Ig2, where Ig1 has magnitude $\frac{\sqrt{2}}{25}$ and Ig2 is given to be 40 mA (no angle). Can you write an equation that represents that?

 

[gruba]

So that will be the magnitude of the current that you get when you sum Ig1 and Ig2, where Ig1 has magnitude $\frac{\sqrt{2}}{25}$ and Ig2 is given to be 40 mA (no angle). Can you write an equation that represents that?

Applying Kirchhoff's first law in the second case, for node 1, $I_1=I_{g1}+I_{g2}=\frac{1+\sqrt 2}{25}A$.

 

[gneill]

No, at this point we're introducing a phase angle for Ig1. Up to now we've only had to deal with current magnitudes and power. Now we are adding in a new current that doesn't have the same phase angle. When you add two sinewaves of the same frequency but differing phase you end up with a new sinewave whose magnitude depends upon the original magnitudes and the phase difference.

So let the new Ig2 = 40 mA current set the reference angle and assign some angle θ to Ig1. You have the magnitude of Ig1 and the magnitude of Ig2 and you know the magnitude of the resulting current you want when they are summed. Find the angle θ that makes this so.

 

[gruba]

So let the new Ig2 = 40 mA current set the reference angle and assign some angle θ to Ig1. You have the magnitude of Ig1 and the magnitude of Ig2 and you know the magnitude of the resulting current you want when they are summed. Find the angle θ that makes this so.

I am not sure if I understood you correctly:

We have $\underline{I_{g1}}+\underline{I_{g2}}=\underline{{I_{g1}}^{'}}$ where
$$\underline{I_{g1}}=\frac{\sqrt 2}{25}e^{j\theta}A,\underline{I_{g2}}=\frac{1}{25}A,\underline{{I_{g1}}^{'}}=\frac{1}{25}A$$.

This gives the equation $$\frac{\sqrt 2}{25}e^{j\theta}+\frac{1}{25}=\frac{1}{25}\Rightarrow e^{j\theta}=0$$
that doesn't have a solution.

I assume that the values are wrong?

 

[gneill]

You're almost there. You want the magnitude of the resulting current to be 1/25. You're not concerned with the final phase angle of the resulting current, just its magnitude. So to modify your equation accordingly:

$\left| \frac{\sqrt 2}{25}e^{j\theta}+\frac{1}{25} \right|=\frac{1}{25}$

Hint: expand $e^{jθ}$ via Euler's formula. There will be a bit of algebra involved involving trig functions.

 

[gruba]

You're almost there. You want the magnitude of the resulting current to be 1/25. You're not concerned with the final phase angle of the resulting current, just its magnitude. So to modify your equation accordingly:

$\left| \frac{\sqrt 2}{25}e^{j\theta}+\frac{1}{25} \right|=\frac{1}{25}$

Hint: expand $e^{jθ}$ via Euler's formula. There will be a bit of algebra involved involving trig functions.

$$e^{j\theta}=\cos\theta +j\sin\theta\Rightarrow \left|\frac{\sqrt 2}{25}e^{j\theta}+\frac{1}{25}\right|=\sqrt{\frac{3+2\sqrt{2}\cos\theta}{625}}$$
$$\Rightarrow\sqrt{{3+2\sqrt{2}\cos\theta}}=1\Rightarrow 3+2\sqrt 2\cos\theta=1\Rightarrow \cos\theta =-\frac{1}{\sqrt 2}$$
$\Rightarrow \theta=\frac{7\pi}{4}$ or $\Rightarrow \theta=-\frac{\pi}{4}$

where $\theta$ is the phase angle difference between $\underline{I_{g1}}$ and $\underline{I_{g2}}$.

 

[gneill]

I think you've done well right up to the end. Check to see if you get a negative cosine for your angle.

Note that there should be two candidate angles that will yield the required cosine. One in quadrant 2 and one in quadrant 3.

 

[gruba]

Note that there should be two candidate angles that will yield the required cosine. One in quadrant 2 and one in quadrant 3.

You are right: $\theta=\frac{3\pi}{4}$ or $\theta=\frac{5\pi}{4}$.

 

[gneill]

Yup, or $\pm \frac{3}{4} \pi$ . Phase angles are conventionally given in the range -180° to +180°.

You should confirm that the resulting total current yields half the power as the original current, say by determining the active power dissipated in Z1.

 

[gruba]

Thanks for the help.

 

[gneill]

You're welcome!