Yossi33
- 22
- 3
- Homework Statement
- newtons second law and multiple pulley problem.
- Relevant Equations
- f=ma
hi,i have this question :
m1=3kg m2=6kg m3=20kg
there is no friction between m3 and the floor.
what is the acceleration of each block?
my attempt is :
the pulley that moves is moving downward at the acceleration of m3.
so the system of m1,m2 is moving downward at the acceleration of m3, then i exerted a "ghost force" on that system that works upward and it works on m1 with magnitude of m1a* and on m2 with magnitude m2a*
then i solved their acceleration as they are not in accelerating system:
m2g-T-m2a*=m2a (1)
T+m1a*-m1g=m1a (2)
the moving pulley is 2T=T* (3)
and of m3 ----> T*=m3a* (6)
if i add 1 +2 --> m2g-m2a*+m1a*-m1g=(m1+m2)a
(m2-m1)g-(m2-m1)a*=(m1+m2)a / divide by (m2-m1)
g-a*=(m1+m2)/(m2-m1) multiply a
g-a*=3a (4)
then i subtitue (4) in (2) ----> T=m1(a-a*+g)
T=3(g/3 -a*/3 -a* +g)
T=4g-4a* (5)
subtitue (5) and (6) in (4)
8g-8a*=m3a*
8g=28a*
a*=8g/28 (7)
subtitue (7) in (4) ---> g/3-8g/78=a
i don't have answers, so please tell me if I am wrong and if i am, then how should i solve this. thank you
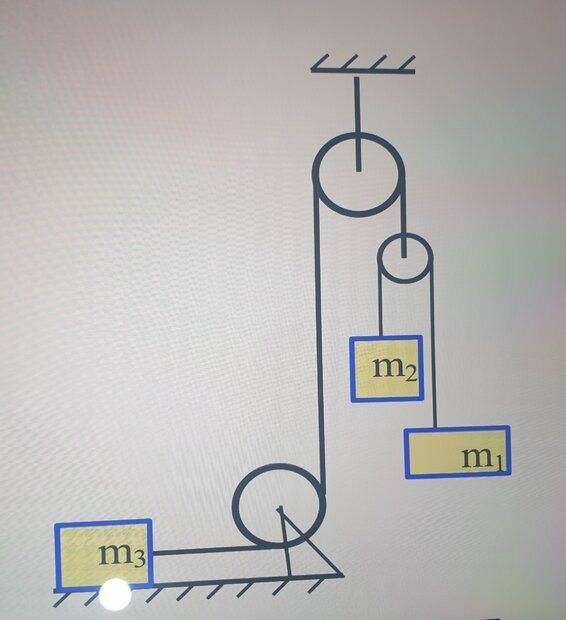
m1=3kg m2=6kg m3=20kg
there is no friction between m3 and the floor.
what is the acceleration of each block?
my attempt is :
the pulley that moves is moving downward at the acceleration of m3.
so the system of m1,m2 is moving downward at the acceleration of m3, then i exerted a "ghost force" on that system that works upward and it works on m1 with magnitude of m1a* and on m2 with magnitude m2a*
then i solved their acceleration as they are not in accelerating system:
m2g-T-m2a*=m2a (1)
T+m1a*-m1g=m1a (2)
the moving pulley is 2T=T* (3)
and of m3 ----> T*=m3a* (6)
if i add 1 +2 --> m2g-m2a*+m1a*-m1g=(m1+m2)a
(m2-m1)g-(m2-m1)a*=(m1+m2)a / divide by (m2-m1)
g-a*=(m1+m2)/(m2-m1) multiply a
g-a*=3a (4)
then i subtitue (4) in (2) ----> T=m1(a-a*+g)
T=3(g/3 -a*/3 -a* +g)
T=4g-4a* (5)
subtitue (5) and (6) in (4)
8g-8a*=m3a*
8g=28a*
a*=8g/28 (7)
subtitue (7) in (4) ---> g/3-8g/78=a
i don't have answers, so please tell me if I am wrong and if i am, then how should i solve this. thank you
Last edited by a moderator: