Acceleration in a pulley system

[KatrineRav]

Homework Statement

Two objects are suspended in a pulley system. Their masses are identical (but I've called them m1 and m2 through most of the calculations). A force is applied to one of the objects. What is the resulting acceleration of that object?

Relevant Equations

F=ma
Fg=mg

SOLUTION ATTEMPT

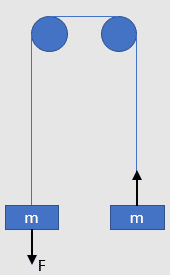
Newtons 2nd law states that F=ma (eq. 1). When a force is applied to a mass m it results in an acceleration a=F/m (eq. 2). If a vertical force is applied to one of the objects in this system, acceleration of both objects will occur. Assuming the length of the rope is constant, a vertical acceleration of object 1 will result in a vertical acceleration of object 2 of equal magnitude but opposite direction, that is a1= - a2 (eq. 3). To calculate the acceleration resulting from a vertical force applied to one of the objects, equation 2 is substituted into equation 3 and then equation 1 is substituted in, giving

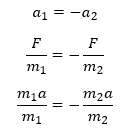
The acceleration a is then isolated giving

--------------------------------
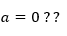
SOLUTION ATTEMPT 2:
Not really an attempt, but I've looked into acceleration problems, where the objects suspended under the pulley has different masses (m1 and m2, m2>m1).
There the acceleration is calculated by

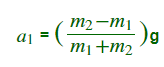
I guess the extra force applied could be expressed as a mass equivalent m_eq=F/g. I could then substitute m2 for m1+m_eq. But that seems like an odd way to go around it...
---------------------------
SOLUTION ATTEMPT 3:
I've also tried to look at the forces applied to each object.
Object 1: gravity (down, -mg), tension (up, T), "the extra force" (down, -F)
Object 2: gravity (down, -mg), tension (up, T)

I tried some different ways of juggling that around but with no luck.
---------------------------
My intuitive understanding is that the answer will be
a=F/(m1+m2)
In this case m1 = m2 and I substitute them for m:
a=F/2m

That makes sense to me, because the two objects are connected, which means that if you apply a force to one of them you are in fact trying to accelerate both of them, which means you have to look at their combined mass to calculate the resulting acceleration.

I just can't seem to get their or any!
Please help :)

 

[kuruman]

Your attempt 3 looks promising. Can you write down a system of two equations and two unknowns and solve for the acceleration $a$ relying on algebra rather than intuition?

 

[KatrineRav]

Uh! I think I got it :) Does this look right?
If we look at the forces applied to each object we get

Using Newtons 2nd law of motion, we setup equations for acceleration of object the objects:

But the tension force is unknown. To determine the tension force we use the fact that -a1=a2 and substitute in the accelerations:

We the isolate T:

And substitue that into eq. 1:

We now see that a1= -F/2m

 

[haruspex]

We now see that a1= -F/2m

Yes, except that if F is shown as positive down then you should take a as positive down as well.

 

[kuruman]

Yes, except that if F is shown as positive down then you should take a as positive down as well.

I see the problem here as an internal inconsistency.
Equation (1) says
$ma_1=-mg+T-F$.
The right side is consistent with the convention "up is positive" and "down is negative" as the applied force and the weight, which defines "down", have the same sign. For the equation to hold, $a_1$ on the left side must be interpreted as an algebraic quantity that can be positive or negative depending on the balancing of forces on the right side. So far so good.
The third equation is
$-a_1=a_2$
It is meant to express the condition that the acceleration vector of one mass is in the opposite direction as the acceleration vector of mass 2. Formally this is derived from the one-dimensional condition $-a_1~\hat y=a_2~\hat y$ by dropping the unit vectors. However, $a_1$ and $a_2$ in the above condition stand or the magnitudes of the vectors, not the signed components. Hence, the internal inconsistency.

To make the two equations consistent, the sign of $a_1$ must be flipped in either one of the two. Note that this inconsistency is akin to the pitfall of correctly writing $T-mg = -ma$ for a mass at the end of a string accelerating down and then substituting $- 9.81~\rm{m/s^2}$ for $g$.

 

[KatrineRav]

Thanks to both of you!
I will fix the inconsistency :)

 

[KatrineRav]

I have a few other questions to this system.
I have described my ideas about the behaviour of this system.
I have marked the ideas about which I am uncertain with bold :)

I use this diagram to simulate a system in which a person/subject is suspended in the left side and a counterweight is suspended in the right side.

Figure 5
Figure 5 shows how a subject accelerates when a force is exerted on them. In 0 g (figure 5a), the force would result in an acceleration of a=f/m. In this setup (figure 5b and c), the same force would theoretically result in an acceleration a=f/2m, half the size of that in 0 g. To achieve the same acceleration as in 0 g, double the force must be applied. This is because of the added inertia of the counterweight, that also must be accelerated. The added inertia of the counterweights makes this setup dissimilar to 0 g.

The theoretical system acceleration of a=f/2m, was based on the assumption that the pulleys and ropes were massless. They are not. The added inertia of the rope and pulleys means the acceleration resulting from a force will be even lower.

The theoretical system acceleration of a=f/2m, was also based on the assumption that a force applied to the subject would be transferred through rope tension to the counterweight. This assumption was close to true, when the subject was moving downwards, resulting in increased tension in the rope and an upwards pull on the counterweight. The high inertia of the system was only felt by the subject when moving downwards.

When the subject was moving upwards, the assumption of transferred forces did not hold true. Since a rope will bend under a compressive load, the upwards force applied by to subject could not “push” the counterweight down. Because of the flexible link between them, the subject was in effect moving independently. This means that a ground reaction force accelerating the subject upwards would result in an acceleration of F=ma. This acceleration would then result in reduced rope tension, resulting in less upwards pull on the counterweight, resulting in a downwards acceleration of the counterweight.

 

[kuruman]

To achieve the same acceleration as in 0 g, double the force must be applied. This is because of the added inertia of the counterweight, that also must be accelerated.

Not true. If you double the force, the equations become
$-ma=mg+T-2F$
$ma=T-mg$
Subtract top equation from bottom
$2ma=2F-2mg~\rightarrow~a=\frac{F}{m}-g$
Clearly, the acceleration is zero when $F=mg$ for the mass on which the force is applied. That's another way of saying that the mass is weightless. Of course the other mass will be in free fall when that happens.

Since a rope will bend under a compressive load, the upwards force applied by to subject could not “push” the counterweight down. Because of the flexible link between them, the subject was in effect moving independently. This means that a ground reaction force accelerating the subject upwards would result in an acceleration of F=ma.

It is true that you cannot "push" with a rope but you need to be careful here. If $F$ is pushing "up" on the subject mass, the rope may still be under tension because of the other mass. As argued above, when the upward $F$ becomes equal to the weight, the subject mass will be moving up with constant velocity and the other mass will be in free fall; if the upward $F$ is greater than the weight, the subject mass will accelerate up and the other mass will still be in free fall. In other words, when the rope is no longer under tension ($F \geq mg$), the masses are decoupled from one another and they will each do their own thing under the influence of whatever net force is acting on them.

 

[KatrineRav]

Thank you very much for that feedback! I will take that into account :)