Sheepwall
- 15
- 0
The problem was present in a physics 1 exam, and I'm reasonably sure I know the answer, yet my friend contradicts me in my conclusion.
Find magnitude of acceleration of system ABC. Masses of A, B and C are all equal and each has mass 2.00 kg. Let gravitational acceleration g = 9.81 m/s2. See figure below.
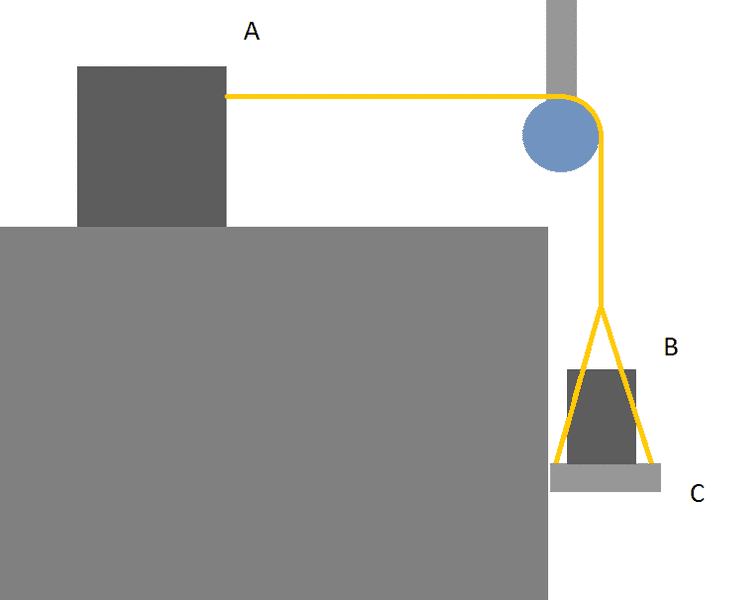
Disregard friction - castor, air, and surface.
Newtons 2nd law of motion:
F = m a (1)
The force on the whole system is gravity's effect on B and C (weight of B and platform C). Through (1):
F = (2)(2.00 kg)(9.81 m/s2) = 39.24 N
Acceleration on the whole system is then, under the above force: (Through (1) again):
a = (39.24 N)/[(3)(2.00 kg)] = 6.54 m/s2.
Obviously, the acceleration of A is directed horizontally, while B and C are accelerating downwards. Still, the acceleration of each objects will be the same, yet in their respective directions. It is this value which I am after.
Also, can someone less ignorant than I tell me if I am right in this:
Without other external forces (other than gravity), the system will never accelerate faster than 9.81 m/s2 and the less the mass of A (and the larger the mass of B and C, equivalently), the closer the systems acceleration will be to 9.81 m/s2.
Thank you in advance and I apologize for the triviality of the problem :s
Homework Statement
Find magnitude of acceleration of system ABC. Masses of A, B and C are all equal and each has mass 2.00 kg. Let gravitational acceleration g = 9.81 m/s2. See figure below.
Disregard friction - castor, air, and surface.
Homework Equations
Newtons 2nd law of motion:
F = m a (1)
The Attempt at a Solution
The force on the whole system is gravity's effect on B and C (weight of B and platform C). Through (1):
F = (2)(2.00 kg)(9.81 m/s2) = 39.24 N
Acceleration on the whole system is then, under the above force: (Through (1) again):
a = (39.24 N)/[(3)(2.00 kg)] = 6.54 m/s2.
Obviously, the acceleration of A is directed horizontally, while B and C are accelerating downwards. Still, the acceleration of each objects will be the same, yet in their respective directions. It is this value which I am after.
Also, can someone less ignorant than I tell me if I am right in this:
Without other external forces (other than gravity), the system will never accelerate faster than 9.81 m/s2 and the less the mass of A (and the larger the mass of B and C, equivalently), the closer the systems acceleration will be to 9.81 m/s2.
Thank you in advance and I apologize for the triviality of the problem :s