maxkor
- 79
- 0
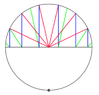
Adam has a circle of radius $1$ centered at the origin.
- First, he draws $6$ segments from the origin to the boundary of the circle, which splits the upper (positive $y$) semicircle into $7$ equal pieces.
- Next, starting from each point where a segment hit the circle, he draws an altitude to the $x$-axis.
- Finally, starting from each point where an altitude hit the $x$-axis, he draws a segment directly away from the bottommost point of the circle $(0,-1)$, stopping when he reaches the boundary of the circle.
What is the product of the lengths of all $18$ segments Adam drew?
- First, he draws $6$ segments from the origin to the boundary of the circle, which splits the upper (positive $y$) semicircle into $7$ equal pieces.
- Next, starting from each point where a segment hit the circle, he draws an altitude to the $x$-axis.
- Finally, starting from each point where an altitude hit the $x$-axis, he draws a segment directly away from the bottommost point of the circle $(0,-1)$, stopping when he reaches the boundary of the circle.
What is the product of the lengths of all $18$ segments Adam drew?