Advanced Hydrodynamic Problem - University level

[Hydro2022]

TL;DR Summary: Advanced hydrodynamic calculation- University Level
Calculate the necessary force of the hydraulic piston to empty the tank located at the bottom in the indicated time.

Hi all guys I'm new on this forum, and I write this post to ask you for help on a mechanical engineering, hydrodynamic, advanced level problem that I am not able to solve and I hope that some of you certainly better than me can to help.

The problem is the following: (I enclose the hydraulic diagram, sorry I know it is not accurate, I did it again on the fly on the PC by copying it from the workbook, unfortunately it is not to scale but it should still be useful to understand the exercise).

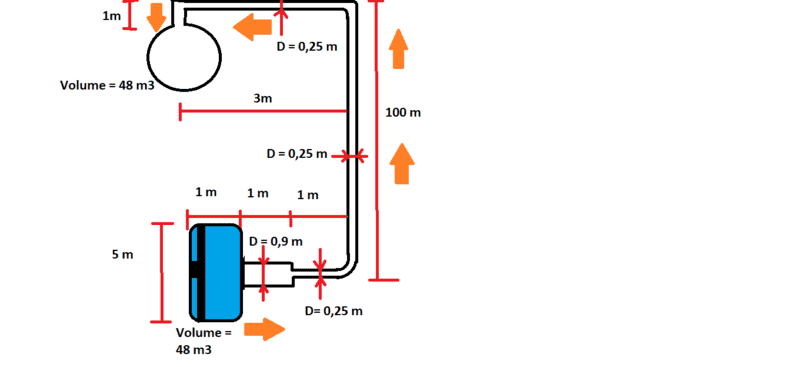
Find the amount of force that must be applied to the hydraulic piston, placed in the blue tank at the bottom, containing 48 thousand liters of water to empty it in 25 seconds through a tube of 0.9m diameter and 1m length which narrows to a 0.25m diameter and 105m length connected up to the spherical tank also of 48 m3 placed at the top.

Fluid density of water at 20 degrees Celsius = 998.21 kg / m ^ 3

Dynamic viscosity of water at 20 degrees Celsius = 0.001002 Pa.s

tank bottom volume 48 m3 (5m * 9.6m * 1m)
while the tank at the top is always 48 m3 but it is spherical

style='font-size:16.0pt;font-family:"inherit",serif;color:#202124;mso-ansi-language:
EN'>='font-size:16.0pt;font-family:"inherit",serif;color:#202124'>

To calculate :

- Total force to be applied to the piston to empty the tank in the indicated time, considering the continuous and localized pressure drops (steel tube with very low roughness) and all frictions.

- Piston power in kWhPractically the piston has a stroke of 1 meter and it is necessary to calculate the force and power of the latter necessary to empty the tank at the bottom completely and consequently fill the spherical tank of the same volume placed at the top.

I tried to solve it, calculating the necessary force and I get about 3000 kN with a power of 1050 kWh, but I don't know where I am wrong and the result does not lead to that of the exercise. I calculated the head losses in the 2 narrowings, in the 3 curves, the continuous head losses and the necessary outflow force from the tank, to calculate the power I first calculated the work but nothing to do.

I thank anyone in advance who can solve the problem and help me.

Thank you :)

 

[Lnewqban]

Welcome @Hydro2022 !

In order to help you, we will need you to show us your calculation work.

It seems to me that your force value should be higher than 3000 kN, considering only the hydrostatic pressure of 9.81 kPa exerted by a 100 m high non-moving water column that should be statically loading the 5.0 m x 9.6 m rectangular face of the piston.

The above is assuming the pipe is full between both tanks and that the spherical top tank is vented to the atmosphere.

Also, the problem does not ask for power, which units are not kWh, which belong to energy or work.

 

[Hydro2022]

@Lnewqban Hello, sorry
you are right I have not attached the calculations;
Practically for carrying out the exercise in the calculation of the Force, I divided the problem into 5 points:

- Point A -> calculate the force necessary to move the mass of 48 thousand liters + force of outflow from the tank to the pipe. I calculated the area of the pipe of D = 0,9m then 0,635 m2 from the area I got the space by making Volume / Area then the 48 m3 of the tank / 0,635 m2 = 76 m. I then calculated the speed by making the space so the 76 meters / 25 seconds = 3 m / s.
From speed with the formula E = 1/2 * m * v ^ 2 = 0.5 * 48000 kg * (3m / s) ^ 2 = 216000 joules.
By dividing the energy by the space covered by the piston which is 1 meter, I obtain the necessary force therefore always 216000N.

- Point B -> calculation of localized losses of the narrowing from a diameter of 0.9 m to 0.25m + the 3 bends present in the pipeline. With the Darcy formula Ya = Sa * (v) ^ 2 / 2g I calculated the localized head losses, with Sa being a tabulated coefficient. The speed obviously I had to recalculate as the section of the tube narrows so I used Bernouilli with the formula V1 * S1 = V2 * S2, so from 3 m / s at the outlet of the tank in the 0.9 tube it becomes 227 m / s and then increases again when it shrinks to 0.25 m becomes 735 m / s. For the 3 curves that are on the 0.25 m diameter pipe I have always used darcy's formula. The coefficients used are Sa = 4 in the narrowing and 0.6 for the curves. The pressure drop I get is in meters of water column, dividing by 10.2 I get the bars then I convert it into Pascal. Knowing the surface and the pressure then I obtain the applied force.

- Point C -> calculation of continuous head losses, for the first section of 0.9 m in diameter and length of 1 meter I have not calculated them as they are negligible given the modest length of the pipe, while in the section of 0.25 in diameter and length 105 meters I first calculated the number of reynolds with the formula Re = (speed * Diameter * Density) / viscosity I get a number of reynolds over 300 Ml due to the high speed of the flow and therefore turbulent motion.
From then with the formula J = F friction * (1 / D) * Density * (V ^ 2) / 2 * pipe length I calculated the continuous pressure drop. Here too, as in the localized ones, I divide by 10.2, thus converting from meters of water column to bars, then dividing 100000 by Pascal and knowing the pressure and surface I get the force.

- Point D -> minimum force to move the mass of water, in this case the calculation is simple as the 48000 kg of water correspond to 470880 N (obtained by making mass * g).- Point E -> hydrostatic pressure, I then calculated with the Stevino formula, the force exerted by the water column in the pipe section 0.25m in diameter and 100m long. So P = q * g * H = 997 kg / m3 * 9.81 m / s2 * 100 m = 978057 Pascal. With the 0.25m diameter I then calculated the area 0.049 m2. The force is therefore F = P * S = 978057 Pascal * 0.049 m2 = 47925 N

In total I have:

- A -> 216 kN
- B -> 1500 kN pressure drop narrowing + 400N pressure drop 3 curves
- C -> 414 kN continuous head losses
- D -> 470 kN minimum force to move the mass of water
- E -> 48 Kn hydrostatic pressure of the water column

In total I get 2650 kN not 3000 kN as I wrote on the comment above I was wrong before sorry, it's just that I'm not understanding anything about this problem anymore.

as far as power is concerned, the problem asks for the value in kwh of the power of the piston that pushes the water, but i don't know exactly how to calculate it also because i have not sufficient dates

 

[Hydro2022]

For the tank at the top it does not have a vent with the atmosphere but is closed,

 

[Hydro2022]

does anyone know how much is the exact force in Newtons that the piston has to exert to push the water out of the tank at the bottom?

 

[Chestermiller]

I don't understand what 300 MI means for the Reynolds number. I get a Re of $9.76\times 10^6$ in the 0.25 m duct.

To empty the 48 m^3 tank in 25s involves a volume flow rate of 1.92 m^3/s. For a 0.9 m diameter tube, this results in a velocity of 3.02 m/s. For a tube diameter of 0.25 m, it results in a flow velocity of 39.1 m/s.

I don't know where you got your numbers in part C from.

 

[Lnewqban]

For the tank at the top it does not have a vent with the atmosphere but is closed,View attachment 316395View attachment 316394

In that case, the piston has also to use additional force and energy to compress 48 cubic meters of air from atmospheric pressure (I assume) up to a value than needs to be calculated as final pressure above the surface.

Perhaps the problem expects that fact to be considered, as well as the volume of the pipe system (initially empty, I again assume) to be filled up (which will be the volume of the air pocket remaining on the top of the surface in the spherical tank at the end of the piston's stroke).

In both cases, you have an increasing gradient of pressure to deal with; therefore, the force on the piston will vary from beginning to end of the 25-minute stroke (but I see that the problem question asks about "the amount of force that must be applied to the hydraulic piston".
Could that mean average force?

Are those questions that you can ask your professor, before diving into the associate complexities?
Have you copied the text of the problem exactly?
Thank you for posting your work.

 

[Hydro2022]

In that case, the piston has also to use additional force and energy to compress 48 cubic meters of air from atmospheric pressure (I assume) up to a value than needs to be calculated as final pressure above the surface.

Perhaps the problem expects that fact to be considered, as well as the volume of the pipe system (initially empty, I again assume) to be filled up (which will be the volume of the air pocket remaining on the top of the surface in the spherical tank at the end of the piston's stroke).

In both cases, you have an increasing gradient of pressure to deal with; therefore, the force on the piston will vary from beginning to end of the 25-minute stroke (but I see that the problem question asks about "the amount of force that must be applied to the hydraulic piston".
Could that mean average force?

Are those questions that you can ask your professor, before diving into the associate complexities?
Have you copied the text of the problem exactly?
Thank you for posting your work.

yes it is exactly as you said, the problem is that I do not know how to calculate the force necessary to push even the 48 m3 of air at atmospheric pressure, my intent was first to calculate the force to move the water then add that of the air. With regard to the necessary force, it means the maximum force that the piston will have to exert therefore at the maximum of the increasing gradient that will occur from the beginning to the end of the 25 seconds of the piston stroke.

i am still trying to figure out how to calculate all this, i also tried to search on the internet but i did not find anything

anyway thank you very much for your answer which clarified part of the exercise for me :)

 

[Hydro2022]

I don't understand what 300 MI means for the Reynolds number. I get a Re of $9.76\times 10^6$ in the 0.25 m duct.

To empty the 48 m^3 tank in 25s involves a volume flow rate of 1.92 m^3/s. For a 0.9 m diameter tube, this results in a velocity of 3.02 m/s. For a tube diameter of 0.25 m, it results in a flow velocity of 39.1 m/s.

I don't know where you got your numbers in part C from.

hello yes double-checking the calculations it is true, you are right, I have the wrong speed and consequently on point C the Reynolds number is wrong, your calculation is correct. My doubt is in addition to the continuous and localized pressure drops, the hydrostatic pressure, are there other factors that I have not considered in your opinion in calculating the force required by the piston to empty the tank?

Anyway thanks for your correction :)

 

[Chestermiller]

hello yes double-checking the calculations it is true, you are right, I have the wrong speed and consequently on point C the Reynolds number is wrong, your calculation is correct. My doubt is in addition to the continuous and localized pressure drops, the hydrostatic pressure, are there other factors that I have not considered in your opinion in calculating the force required by the piston to empty the tank?

Anyway thanks for your correction :)View attachment 316448

The main thing you need to calculate is the pressure in the tank. To get the force, you just multiply by the cross sectional area.

The changes in calculation of velocities also affects the calculations in A and B.

Item D shouldn't be included; I have no idea what that is supposed to be.

 

[Lnewqban]

yes it is exactly as you said, the problem is that I do not know how to calculate the force necessary to push even the 48 m3 of air at atmospheric pressure, my intent was first to calculate the force to move the water then add that of the air. With regard to the necessary force, it means the maximum force that the piston will have to exert therefore at the maximum of the increasing gradient that will occur from the beginning to the end of the 25 seconds of the piston stroke.

i am still trying to figure out how to calculate all this, i also tried to search on the internet but i did not find anything

View attachment 316447anyway thank you very much for your answer which clarified part of the exercise for me :)

View attachment 316446View attachment 316445

Your receiving tank will end up with compressed air inside.
Your piston will pump a column of water.
At the end of the stroke, your piston must be resisting the increased pressure of the pocket of air plus the static column of water.

An instant before the end of the stoke, your piston will have to overcome the additional resistance of 48 cubic meters of water quickly moving inside the pipes.

Run those three calculations of pressure (two static and one dynamic), and add them all.
Then, the total pressure to overcome will give you the max pushing force of the piston.
Work and power calculation should consider the variation of pressure regarding stroke distance and time.

Could you share the solution values given in the textbook?

 

[Chestermiller]

Your receiving tank will end up with compressed air inside.
Your piston will pump a column of water.
At the end of the stroke, your piston must be resisting the increased pressure of the pocket of air plus the static column of water.

An instant before the end of the stoke, your piston will have to overcome the additional resistance of 48 cubic meters of water quickly moving inside the pipes.

Run those three calculations of pressure (two static and one dynamic), and add them all.
Then, the total pressure to overcome will give you the max pushing force of the piston.
Work and power calculation should consider the variation of pressure regarding stroke distance and time.

Could you share the solution values given in the textbook?

I think the OP indicated that the upper tank is vented to the atmosphere.

 

[Lnewqban]

I think the OP indicated that the upper tank is vented to the atmosphere.

Please, refer to post #4 above.

 

[Chestermiller]

I must’ve missread post number 4. Still doesn’t make sense unless the tank at the top is vented to the atmosphere.

 

[erobz]

This problem seems very under designed to me. I'm having trouble believing this wasn't just made up. You have to compress the air volume (piping + upper tank) into a volume that is effectively the volume of the piping. Assuming $P_o = P_{atm}$ , that's like a final pressure of $9 \rm{atm}$. The piston has an area of about $50 \rm{m^2}$ if I've estimated properly that is $4.5 \cdot 10^7 N$! Just the force from that increase in gas pressure alone is absolutely tremendous. Also, because of this the flow will be unsteady. None of the standard (simplified) approaches for calculating head loss can be used.

I don't buy it.

 

[Lnewqban]

The piston has an area of about $50 \rm{m^2}$ if I've estimated properly that is $4.5 \cdot 10^7 N$!

In order to displace that volume with a stroke of 1 m, the piston must have a 5.0 m x 9.6 m rectangular face.

 

[Hydro2022]

Your receiving tank will end up with compressed air inside.
Your piston will pump a column of water.
At the end of the stroke, your piston must be resisting the increased pressure of the pocket of air plus the static column of water.

An instant before the end of the stoke, your piston will have to overcome the additional resistance of 48 cubic meters of water quickly moving inside the pipes.

Run those three calculations of pressure (two static and one dynamic), and add them all.
Then, the total pressure to overcome will give you the max pushing force of the piston.
Work and power calculation should consider the variation of pressure regarding stroke distance and time.

Could you share the solution values given in the textbook?

the results in the book are force = 11100 N and piston power 660 kWh

 

[Hydro2022]

The main thing you need to calculate is the pressure in the tank. To get the force, you just multiply by the cross sectional area.

The changes in calculation of velocities also affects the calculations in A and B.

Item D shouldn't be included; I have no idea what that is supposed to be.

for the point I was not sure in fact, I had also considered the weight force in the calculation therefore the mass of the water that the piston must move therefore 48 thousand liters correspond to 470880 Newton, at this point seen which is not to be considered I eliminate it from the calculations

 

[Hydro2022]

The main thing you need to calculate is the pressure in the tank. To get the force, you just multiply by the cross sectional area.

The changes in calculation of velocities also affects the calculations in A and B.

Item D shouldn't be included; I have no idea what that is supposed to be.

ok i didn't consider the problem in this way, ok i calculated the pressure inside the tank with stevino's law P = q * g * h = 1000 kg / m3 * 9.81 m / s2 * 5m = 48903 Pascal. I then multiplied this pressure by the area of the tank 48 m2 and I obtained a force of 2347 kN so excluding the air and the pressure drops is this the force that the piston must exert?

 

[Hydro2022]

This problem seems very under designed to me. I'm having trouble believing this wasn't just made up. You have to compress the air volume (piping + upper tank) into a volume that is effectively the volume of the piping. Assuming $P_o = P_{atm}$ , that's like a final pressure of $9 \rm{atm}$. The piston has an area of about $50 \rm{m^2}$ if I've estimated properly that is $4.5 \cdot 10^7 N$! Just the force from that increase in gas pressure alone is absolutely tremendous. Also, because of this the flow will be unsteady. None of the standard (simplified) approaches for calculating head loss can be used.

I don't buy it.

ok thanks for your answer, I didn't decide the exercise, unfortunately it was only assigned to me by our professor so I can't tell you why it sounds strange to you

 

[Hydro2022]

This problem seems very under designed to me. I'm having trouble believing this wasn't just made up. You have to compress the air volume (piping + upper tank) into a volume that is effectively the volume of the piping. Assuming $P_o = P_{atm}$ , that's like a final pressure of $9 \rm{atm}$. The piston has an area of about $50 \rm{m^2}$ if I've estimated properly that is $4.5 \cdot 10^7 N$! Just the force from that increase in gas pressure alone is absolutely tremendous. Also, because of this the flow will be unsteady. None of the standard (simplified) approaches for calculating head loss can be used.

I don't buy it.

ok that is the force only to compress the air instead the force only to compress the water how much would it be?

 

[erobz]

ok that is the force only to compress the air instead the force only to compress the water how much would it be?

View attachment 316510

Firstly, if you are compressing the gas, the force varies in time. So, asking for "the force" doesn't make sense? The force would start out as "back pressure" from viscous losses. That viscous loss back pressure would be quickly dominated by the increasing pressure of the gas.

If the answer in the book is a constant - $11,100 \rm{N}$, then this system has to be vented, and the flow is assumed steady.

 

[Hydro2022]

at this point seeing that the result is to you where the force is much greater than the result, it makes me think then that I was wrong and the tank at the top is open, but heck it is not written anywhere that it is open on the exercise and also from the scheme that I have copied you can see that it is closed, I am having a doubt now

 

[Hydro2022]

Firstly, if you are compressing the gas, the force varies in time. So, asking for "the force" doesn't make sense? The force would start out as "back pressure" from viscous losses. That back pressure would be quickly dominated by the increasing pressure of the gas.

If the answer in the book is a constant - $11,100 \rm{N}$, then this system has to be vented, and the flow is assumed steady.

at this point seeing that the result is to you where the force is much greater than the result, it makes me think then that I was wrong and the tank at the top is open, but heck it is not written anywhere that it is open on the exercise and also from the scheme that I have copied you can see that it is closed, I am having a doubt now

View attachment 316511

then it must be as you say but how the exercise is written in the book was not clear, this problem is making my hair white I can't take it anymore :( :(

 

[Hydro2022]

in any case I do not understand how the result can be 11100 kN when, even adding all the forces I have calculated, I do not exceed 3000 kN

 

[erobz]

If you assume its vented and the flow is steady (which would be the application of a constant force to the piston), then you can apply the "Energy Equation" (conservation of energy for viscous fluid flows). I'm guessing that is the intention of the author. I'm still not sold though because the pipe is initially empty, or perhaps it isn't?

 

[Hydro2022]

@erobz sorry to Energy Equation (conservation of energy) do you mean Bernouilli right ?

 

[erobz]

in any case I do not understand how the result can be 11100 kN when, even adding all the forces I have calculated, I do not exceed 3000 kN

View attachment 316513

You wrote that the answer was $11,100 \, \rm{N}$, which is it?

 

[Hydro2022]

You wrote that the answer was $11,100 \, \rm{N}$, which is it?

the part of the problem it's this

To Calculate:
Total force to be applied to the piston to empty the tank in the indicated time, considering the continuous and localized pressure drops (steel tube with very low roughness) and all frictions.

 

[erobz]

@erobz sorry to Energy Equation (conservation of energy) do you mean Bernouilli right ?

No, in Bernoullis the flow is invisicid. If the flow was inviscid the force on the piston to evacuate the tank at any rate would simply be the weight of the vertical water column + the change in kinetic head from inlet to outlet.

 

[Hydro2022]

No, in Bernoullis the flow is invisicid. If the flow was inviscid the force on the piston to evacuate the tank at any rate would simply be the weight of the vertical water column.

ok thanks for the answer, then it is not enough to calculate reynolds and determine if the motion is turbulent or laminar and consider the frictions accordingly? ok then of the inviscid fluids, this part of physics I think I have never done it

 

[erobz]

ok thanks for the answer, then it is not enough to calculate reynolds and determine if the motion is turbulent or laminar and consider the frictions accordingly? ok then of the inviscid fluids, this part of physics I think I have never done it

View attachment 316515

These are viscous flows. It is like that. You will calculate the Reynolds Number, and refer to the Moody Diagram to determine the friction factor for each section of pipe.The Energy Equation: (It looks like Bernoulli's, but they are different).

$$ \frac{P_1}{\gamma} + z_1 + \alpha\frac{V_1^2}{2g} + h_p = h_t + \frac{P_2}{\gamma} + z_2 + \alpha\frac{V_2^2}{2g} + \sum_{1 \to 2} h_{loss} $$

$h_p$ is pump head
$h_t$ is turbine head
$\alpha$ is the kinetic energy correction factor (turbulent flow $\alpha \approx 1.05$ , laminar flow $\alpha = 2$)
$\sum h_{loss}$ is the total head loss between $(1)$ to $(2)$

You are also going to use continuity for incompressible flow:

$$Q = V_1 A_1 = V_2 A_2$$

You are going to simplify what is above, and solve for $P_1$, which will be the pressure acting over the surface of the piston.

 

[Hydro2022]

These are viscous flows. It is like that. You will calculate the Reynolds Number, and refer to the Moody Diagram to determine the friction factor for each section of pipe.The Energy Equation: (It looks like Bernoulli's, but they are different).

$$ \frac{P_1}{\gamma} + z_1 + \alpha\frac{V_1^2}{2g} + h_p = h_t + \frac{P_2}{\gamma} + z_2 + \alpha\frac{V_2^2}{2g} + \sum_{1 \to 2} h_{loss} $$

$h_p$ is pump head
$h_t$ is turbine head
$\alpha$ is the kinetic energy correction factor (turbulent flow $\alpha \approx 1.05$ , laminar flow $\alpha = 2$)
$\sum h_{loss}$ is the total head loss between $(1)$ to $(2)$

You are also going to use continuity for incompressible flow:

$$Q = V_1 A_1 = V_2 A_2$$

You are going to simplify what is above, and solve for $P_1$, which will be the pressure acting over the surface of the piston.

ok thank you very much for the formula you are really helping me to solve the problem I am getting closer to the solution, but hp and ht where I find these data because I don't have a pump or a turbine in the problem/hydraulic scheme :)

 

[erobz]

ok thank you very much for the formula you are really helping me to solve the problem I am getting closer to the solution, but hp and ht where I find these data because I don't have a pump or a turbine in the problem/hydraulic scheme :)

If there is no pump or turbine between the points of interest i.e. the outlet of lower tank and inlet of upper tank, then those terms are zero.

 

[Hydro2022]

If there is no pump or turbine between the points of interest i.e. the outlet of lower tank and inlet of upper tank, then those terms are zero.

ok thank you very much now I try to calculate with this formula, just a last thing sorry

the y in the image here attached (sorry but on the keyboard i don't know how to write it) what it is ? and Z it is the piezometric height right ? in this case would be 100 m the maximum height that the water reaches ? Am I correct ?
sorry to ask so many questions but as you can see I am really bad at physics :(

 

[erobz]

ok thank you very much now I try to calculate with this formula, just a last thing sorry View attachment 316536
the y in the image here attached (sorry but on the keyboard i don't know how to write it) what it is ? and Z it is the piezometric height right ? in this case would be 100 m the maximum height that the water reaches ? Am I correct ?
sorry to ask so many questions but as you can see I am really bad at physics :(

View attachment 316537

$\gamma$ (gamma) is the specific weight of the fluid. $\gamma = \rho g$

$z$ is the static elevation head for the point of reference. I would take $z_1 = 0$.

 

[Hydro2022]

@erobz
I tried to calculate the pressure with the equation but I can't solve it as unfortunately I have two unknowns both P1 that of the tank but also P2 that is the pressure inside the 250 mm diameter pipe. Do you think there is anothe way to calculate the pressure ?

thanks in advance

luckily I have another 2 weeks before I have to submit the exercise

 

[erobz]

$P_2$ is 0 gauge. You should be taking point 1 as the entrance of the 0.9 m diameter pipe. Point 2 should be the exit of the 0.25 m pipe. We are assuming the upper tank is at atmospheric pressure (0 gauge).

The only issue that you would need to split it up for, is if the flow in the large 0.9 m pipe is laminar. We know the flow in the 0.25 m pipe is turbulent.

 

[Hydro2022]

$P_2$ is 0 gauge. You should be taking point 1 as the entrance of the 0.9 m diameter pipe. Point 2 should be the exit of the 0.25 m pipe. We are assuming the upper tank is at atmospheric pressure (0 gauge).

The only issue that you would need to split it up for, is if the flow in the large 0.9 m pipe is laminar. We know the flow in the 0.25 m pipe is turbul

$P_2$ is 0 gauge. You should be taking point 1 as the entrance of the 0.9 m diameter pipe. Point 2 should be the exit of the 0.25 m pipe. We are assuming the upper tank is at atmospheric pressure (0 gauge).

The only issue that you would need to split it up for, is if the flow in the large 0.9 m pipe is laminar. We know the flow in the 0.25 m pipe is turbulent.

@erobz
ok I tried again with the calculation, I eliminated from the equation the factors that are not present in the problem, so z1 / hp / ht / P2 as it is 0.

V1 = 3.02 m / s (speed in the section of 0.9 m) calculated with the flow rate of 1.92 m3 / s
V2 = 39.2 m / s (speed in the section of 0,25m) calculated from the flow rate of 1.92 m3 / s
With these speeds I calculated the continuous and localized pressure drops for a total of 500 meters of water column

in the end the formula comes to me like this

where x = P1

in the end the result is P1 = 6 670 000 Pascal

 

[Hydro2022]

@erobz
this pressure now to get the Force I have to multiply it by which surface? that of the tank therefore 48 m2 or that of the 0.9 m section where the water comes out of the tank?
thank you

 

[Hydro2022]

because if I multiply it by the area with a diameter of 0.9 meters, the result is a force of 4235 kN
while if I multiply it by the surface of the tank comes a monstrous force of 320 000 kN

the first solution is the one that comes closest to the true result of 11,000 kN

 

[Hydro2022]

maybe we are getting closer to the solution I hope so

 

[erobz]

@erobz
this pressure now to get the Force I have to multiply it by which surface? that of the tank therefore 48 m2 or that of the 0.9 m section where the water comes out of the tank?
thank you

View attachment 316768

It should be multiplied by the piston surface area. We are ignoring head losses in the tank.

 

[erobz]

If you completely ignore head losses it comes out to about $\approx 85 \cdot 10^3 \, \rm{kN}$. Clearly there is a serious issue.

The static elevation head alone is well over the supposed answer.

$$F_{z} = z_2 \cdot \rho \cdot g \cdot A = 100 \rm{m} \cdot 997 \rm{\frac{kg}{m^3}} \cdot 9.81 \rm{\frac{m}{s^2}} \cdot 48\rm{m^2} \approx 47 \cdot 10^3 \rm{kN}$$

 

[Hydro2022]

If you completely ignore head losses it comes out to about $\approx 85 \cdot 10^3 \, \rm{kN}$. Clearly there is a serious issue.

The static elevation head alone is well over the supposed answer.

$$F_{z} = z_2 \cdot \rho \cdot g \cdot A = 100 \rm{m} \cdot 997 \rm{\frac{kg}{m^3}} \cdot 9.81 \rm{\frac{m}{s^2}} \cdot 48\rm{m^2} \approx 47 \cdot 10^3 \rm{kN}$$

thank you very much for your answer I really appreciate your help, I will try to understand why the result is much lower than the monstrous value we get

 

[erobz]

thank you very much for your answer I really appreciate your help, I will try to understand why the result is much lower than the monstrous value we get

View attachment 316781

I don't think you are going to be able too. Are you sure it's not $110,000 \, \rm{kN}$? What I showed was simply the force on the cylinder to simply hold the $100 \rm{m}$ column statically was practically 5 times the quoted result of $11,000 \rm{kN}$. That is as low as the force could possibly get. The result of $11,000 \rm{kN}$ is unattainable.

 

[Hydro2022]

If you completely ignore head losses it comes out to about $\approx 85 \cdot 10^3 \, \rm{kN}$. Clearly there is a serious issue.

The static elevation head alone is well over the supposed answer.

$$F_{z} = z_2 \cdot \rho \cdot g \cdot A = 100 \rm{m} \cdot 997 \rm{\frac{kg}{m^3}} \cdot 9.81 \rm{\frac{m}{s^2}} \cdot 48\rm{m^2} \approx 47 \cdot 10^3 \rm{kN}$$

only a doubt, in the calculation of the hydrostatic force of 47 000 kN, the force is vertical, why the surface of the 0.25 m is not considered but is multiplied by the entire surface of the tank? the force does not act vertically at the base of the tube of 0,25 m?

 

[erobz]

only a doubt, in the calculation of the hydrostatic force of 47 000 kN, the force is vertical, why the surface of the 0.25 m is not considered but is multiplied by the entire surface of the tank? the force does not act vertically at the base of the tube of 0,25 m?View attachment 316785

You need to review hydrostatic pressure if you are having conceptual difficulty with that part. You should be well beyond that in coursework if you are expected to solve these problems.

 

[Lnewqban]

only a doubt, in the calculation of the hydrostatic force of 47 000 kN, the force is vertical, why the surface of the 0.25 m is not considered but is multiplied by the entire surface of the tank? the force does not act vertically at the base of the tube of 0,25 m?View attachment 316785

The diameter of the pipes carrying the flowing water are only relevant when estimating the resistance that those present to that flow.
Only the height of the vertical column of water matters, regarding hydrostatic (non-moving fluid) pressure.

Please, see:
https://en.wikipedia.org/wiki/Torricelli's_law

https://en.wikipedia.org/wiki/Pascal's_law

Not considering the final pressure of the compressed air in the spherical top tank (assuming that the top tank is open to the atmosphere), the value of the static pressure along the horizontal line that runs through the centers of the blue tank, the 0.9 m diameter pipe and the horizontal section and elbow of the 0.25 m diameter pipe would be the same: $980.64~kPa$ or $980.64~N/m^2$.

Since $P=F/A$, that pressure would push the $48~m^2$ piston with a force of $47040~kN$.

Yes, the walls of the 0.25 m diameter pipe will be "feeling" that same pressure, as well as the masses of fluid located directly forward and after that section.

Please, see:
https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/14-1-fluids-density-and-pressure/

 

[Lnewqban]

Perhaps the length of the vertical pipe could be 10 meters rather than 100?
A 10-meter water column would induce a static pressure of $98.06 ~kN/m^2$ on the piston.

Please, see attached PDF drawing at scale to appreciate the real dimensions of the problem as shown at post #1.