Hello Alex,
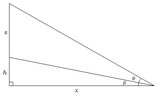
First let's draw a diagram:
View attachment 1638
$$s$$ is the vertical height of the screen in feet.
$$h$$ is the vertical distance from the bottom of the screen to eye level in feet.
$$\theta$$ is the viewing angle, which we wish to maximize.
We see that using the definition of the tangent function, we may write:
(1) $$\tan(\beta)=\frac{h}{x}$$
(2) $$\tan(\beta+\theta)=\frac{h+s}{x}$$
Using the angle-sum identity for tangent, (2) may be expressed as:
$$\frac{\tan(\beta)+\tan(\theta)}{1-\tan(\beta)\tan(\theta)}=\frac{h+s}{x}$$
Using (1), this becomes:
$$\frac{\frac{h}{x}+\tan(\theta)}{1-\frac{h}{x}\tan(\theta)}=\frac{h+s}{x}$$
On the left, multiplying by $$1=\frac{x}{x}$$ we obtain:
$$\frac{h+x\tan(\theta)}{x-h\tan(\theta)}=\frac{h+s}{x}$$
Now we want to solve for $\tan(\theta)$. Cross-multiplying, we find:
$$hx+x^2\tan(\theta)=(h+s)x-h(h+s)\tan(\theta)$$
Adding through by $$h(h+2)\tan(\theta)-hx$$ we get:
$$h(h+s)\tan(\theta)+x^2\tan(\theta)=(h+s)x-hx=sx$$
Factoring the left side:
$$\left(x^2+h(h+s) \right)\tan(\theta)=sx$$
Dividing through by $$x^2+h(h+s)$$ we obtain:
$$\tan(\theta)=\frac{sx}{x^2+h(h+s)}$$
Now, differentiating with respect to $x$ and equating the result to zero to find the critical value(s), we find:
$$\sec^2(\theta)\frac{d\theta}{dx}=\frac{\left(x^2+h(h+s) \right)s-sx(2x)}{\left(x^2+h(h+s) \right)^2}=\frac{s\left(h(h+s)-x^2 \right)}{\left(x^2+h(h+s) \right)^2}=0$$
Multiply through by $$\cos^2(\theta)$$ to get:
$$\frac{d\theta}{dx}=\frac{s\cos^2(\theta)\left(h(h+s)-x^2 \right)}{\left(x^2+h(h+s) \right)^2}=0$$
Since we must have $$\theta<\frac{\pi}{2}$$, our only critical value comes from:
$$h(h+s)-x^2=0$$
Since $$0<x$$ we take the positive root:
$$x=\sqrt{h(h+s)}$$
Using the first derivative test, we see:
$$\left.\frac{d\theta}{dx} \right|_{x=\sqrt{\frac{h}{2}(h+s)}}=\frac{s\cos^2(\theta)\left(h(h+s)-\frac{h}{2}(h+s) \right)}{\left(\frac{h}{2}(h+s)+h(h+s) \right)^2}=\frac{s\cos^2(\theta)\left(\frac{h}{2}(h+s) \right)}{\left(\frac{3h}{2}(h+s) \right)^2}>0$$
$$\left.\frac{d\theta}{dx} \right|_{x=\sqrt{2h(h+s)}}= \frac{s\cos^2(\theta)\left(h(h+s)-2h(h+s) \right)}{\left(2h(h+s)+h(h+s) \right)^2}= -\frac{s\cos^2(\theta)\left(h(h+s) \right)}{\left(3h(h+s) \right)^2} <0$$
Thus, we conclude the critical value is at a maximum for $\theta$.
Now, using the given value $h=3\text{ ft}$, we find the distance $x$ from the screen that maximizes the viewing angle is given by:
$$x=\sqrt{3(3+s)}$$