Algebraic Operations on Differentials in Liebniz Notation: An Abuse?

[chrisr999]

I've seen that myself jgens, and students end up quite confused, those errors are also normally accompanied by numerous other inconsistencies, often using examples that are out of context.

many textbooks are not written by mathematicians.

Many maths teachers are not mathematicians at all, I've seen so many try to correct maths papers handed in by students and you may not believe what I've seen.

I am a mathematician.

You cannot understand calculus without examinig closely what's occurring at those limits

 

[jgens]

Don't get bogged down with whether you are dealing with real numbers, infinitesimals or fractions. Understand the "geometry" behind it.

I certainly understand the geometry behind derivatives and I understand intuitively the concept of a ratio between two infinitessimal numbers. However, moving beyond intuition, it's important to understand the mathematical princples behind calculus. In the real number system, infinitessimals do not exist. Unless you want to rigorously define infinitessimals, work out all of their properties and develop calculus from that number system (I think this is done in nonstandard calculus) you have to abandon the notion of a ratio of infinitessimals.

 

[chrisr999]

the "value" of an "infinitesimal" is an element of the set of positive quotients, which is a subset of the set of real numbers. The "infinitesimal" may be changing in value as you approach a tangent in the case of derivatives. It may even be disappearing, but that's because of how derivatives are "derived".
Check the alternative view of the geometry of the tangent.

Remember the number systems are "representations".
You can work with negative values also but remember you are working with little "lengths" on a diagram when learning differentiation.

You calculate the "value" of the derivative at a real value of the variable.
That locates where you are calculating the specific rate of change of the function at a specific value (real), but the derivative itself is being calculated by examining, in terms of the function equation, the tangent of the angle of the tangent, in other words, the "ratio" of the sides of the "vanishing triangle" which you can magnify and observe it's structure flush against the tangent in the diagram in the .pdf file attached previously.

 

[chrisr999]

Also, "infinitesimals" are just small measurements of the length of a line, that's all.
Don't be concerned about understanding their "properties".
They are lengths on the real number line from zero up to some small value if you want to look at it that way.
Hair widths, tiny differences between two positions, molecular dimensions, whatever way you like to look at it.
Examine as much as you can independently.

 

[jgens]

the "value" of an "infinitesimal" is an element of the set of positive quotients, which is a subset of the set of real numbers.

Really? Infinitessimals are not part of the real number system so they cannot be a subset of the real numbers. Here's how I think that we can show an infinitessimal is not a real number: Suppose k is a positive infinitessimal, then 0 < k < 1/n ∀n ∈ N. However, using limits we can show that there is no positive number k with this property hence, k = 0. While I didn't prove my statement with limits, if you've taken calculus you should be able to do that on your own.

Since this seems to be along the lines of what you're discussing, I figure I'll post these here. Notice that in order to do calculus with infinitessimals you need to introduce several new concepts.

http://en.wikipedia.org/wiki/Hyperreal_number

http://en.wikipedia.org/wiki/Non-standard_calculus

 

[jambaugh]

Here is how I explain this issue with my calculus students. At first we define the derivative which is not a fraction but a limit of a fraction. We prove various limit laws of which the important ones are:
Limits of fraction are fractions of limits (if all limits and expressions are defined).
Limits of products likewise (and especially limits of products of fractions for our purposes)

We then learn the chain rule and observe that though it is not cancellation of fractions mathematically the Leibniz notation for the chain rule seems to follow the form of fraction cancellation. This is a virtue of the Leibniz notation, it does some of our thinking for us by allowing an old algebraic rule, fraction cancellation, to keep track of the new calculus rule, the chain rule.

All the while I am strongly hinting that when we talk about differentials we will better understand the Leibniz notation as being equal too though not defined as a fraction.

Finally we discuss differentials as new variables constructed from old variables which have specific relationships inherited from the relationships we impose on the parent variables. In particular if y = f(x) then dy = f'(x) dx and thus by the definition of the differentials the derivative is indeed equal in value to the ratio of the differentials dy/dx.

We then discuss the differential operator which acts on an expression which we may equate to an implicit dummy variable. The differential of the expression yields the expression which must be equal to the differential of that implicit variable. For example
d(x^2) is just du for u=x^2 and thus du = 2x dx.

I think that we can resolve the "derivatives are fractions" "no they are not" arguments by distinguishing the definition of the derivative (which is a limit of a fraction) from the definition of a differential (which defines them as variables whose ratios are in fact derivatives).

I finish my discussion on differentials by having the students consider the equation:
\frac{dy}{dx} = dy \div dx
The left hand side is Leibniz's notation for a derivative and the right hand side is the ratio of two differentials. Totally different types of objects on each side and the equation itself is not a tautological identity but rather is an implication of the definition of the differentials.

For my students we then revisit the chain rule with this in mind. I find they get a much clearer understanding both of the power of Leibniz notation and in the distinction between differentials and derivatives from this picture. They are thus much better prepared to dive into the integral notation which we hit in the last third of the semester of Calc 1. Not to mention their better ability to deal with implicit differentiation and related rates.

EDIT: Notice that by defining differentials as variables (relative coordinates for a point on a tangent line) there is no need to invoke infinitesimals.

 

[jgens]

Don't be concerned about understanding their "properties".

Here's the problem with this. If you don't fully develop infinitessimals, how can you rigorously develop calculus and how can you be certain that their are no obvious inconsistencies?

 

[jambaugh]

Really? Infinitessimals are not part of the real number system so they cannot be a subset of the real numbers.

You can work with infinitesimals as real numbers. However you need to use an alternative equivalence relationship in the "equations" involving differentials as "infinitesimal quantities".
Allow differentials to be variables which linearly depend on an implicit parameter (we can call epsilon) and treat equations involving differentials as equivalence relations relating limits:

f(x,y,dx,dy) \doteq g(x,y,dx,dy)
translates to:
\lim_{\epsilon \to 0} \frac{f(x,y,dx,dy)}{g(x,y,dx,dy)} = 1
where epsilon is that implicit parameter to which all differentials are assumed to be proportional.

With this treatment there is no need to invoke exotic esoteric "hyper-super-duper-real numbers".

In short the problem with differentials as infinitesimals is not in the infinitesimal concept itself but rather in the sloppy use of = in equations.

 

[jgens]

jambaugh, is it possible to rigorously develop calculus using differentials? I thought that they were more a calculational trick than anything else, but perhaps not?

 

[chrisr999]

Some mistyping is corrected for the .pdf file.

You can consider that they are already developed as they are simply small measurements, with both heading to zero at the same time (the numerator and denominator of the ratio).
The tangent is always there, but you see, the reason we've ended up with the "infinitesimals" is because the "gradient of a line" is vertical distance divided by horizontal distance for a right-angled triangle placed against the line itself, no matter what size the triangle it is since the ratio of the vertical side to horizontal side is constant (tan(angle)), and this "crude" line gradient is then being "tweaked" to rest on top of the tangent.
Differentiation starts out with an "approximation" to the tangent gradient by choosing two points on the curve. This is because we only have the function equation to deal with!
but tilting this line until it "becomes the tangent" cause the numerator and denominator of the line gradient to start disappearing. Examine the diagram in the .pdf file... this is what is happening with the triangles to the right of the tangent. They are there to focus you on how we end up having to evaluate a limit FROM THE FUNCTION EQUATION.
Once you see the triangle disappearing, you switch to the triangles on the left of the tangent, to see exactly what the ratio of the sides are at the limit! It doesn't matter which triangle you examine! the ratio of the sides of the triangle you cannot see is the ratio of the sides of any of those triangles with the angle theta.
You won't be able to understand it without realising why we started out with the triangles on the right of the tangent and ended up with the triangles on the left.
Once you comprehend it visually, you don't need to think in terms of number systems.
Remember "any" number can be "expressed" as a fraction anyway.
Try to "visually understand this using the mathematical way to write a line gradient.
Remember 2 times multiplications can be represented visually as a line through the origin with a gradient of 2 and so on.

 

[HallsofIvy]

Here's the problem with this. If you don't fully develop infinitessimals, how can you rigorously develop calculus and how can you be certain that their are no obvious inconsistencies?

Calculus textbooks from the middle nineteenth century to about 1960, and almost all since 1960, do NOT use infinitesmals to "rigorously develop calculus"- they use limits. Starting about 1960, a new treatment of infinitesmal based calculus was developed as "non-standard Calculus". You won't see it in introductory calculus texts because it uses very deep results from Logic and "model theory" to define "infinitesmals".

jambaugh, is it possible to rigorously develop calculus using differentials? I thought that they were more a calculational trick than anything else, but perhaps not?

Differentials are rigorously defined and used in diffential geometry.

 

[jgens]

Geometically the derivative is not a difficult concept and visually I understand what it means. However, a geometric picture is not good enough in mathematics and when formalizing concepts with rigorous proof, you almost need to forgo geometric intuition completely. This is when number systems come in handy.

 

[jgens]

Calculus textbooks from the middle nineteenth century to about 1960, and almost all since 1960, do NOT use infinitesmals to "rigorously develop calculus"- they use limits. Starting about 1960, a new treatment of infinitesmal based calculus was developed as "non-standard Calculus". You won't see it in introductory calculus texts because it uses very deep results from Logic and "model theory" to define "infinitesmals".

I actually posted a link to the non-standard calculus wiki! My point to chrisr999 was that he had not even developed nor mentioned a rigorous definition of infinitessimals so he could not be sure they were consistent.

Differentials are rigorously defined and used in diffential geometry.

Cool! I learned something new today!

 

[chrisr999]

What we mean by the "limit of a fraction" jgens, is depicted visually on the diagram in the .pdf file. It's a bit like putting a folding ladder against a window. You hoist it and unfold it until it rests safely against the window.

The fraction in question is first the gradient of a line joining two points of a curve.
this gradient does not give you the derivative at the point of tangency! but it's a start as we can use the gradient of a line equation to get going.
then, you bring the second point over to the first. "Unfortunately"! or fortunately in the case of the curious student, the triangle we were working with vamoosed.

At the limit the gradient is the tangent gradient in spite of the fact that the triangle imploded.
If you understand it geometrically, you'll see it all soon enough.

then you will find the mathematical language no different to English.

 

[chrisr999]

No, jgens, the more clear the geometry, the more you realize what is being written in the mathematics language.
Derivatives can be fully understood geometrically, at that point you can "invent" your own mathematical symbols to describe it, but as things stand you should try your best to understand why Leibniz wrote the notation using the format of a ratio.
He did it for a clear reason. There was no notation until it was developed to "describe" whatever it was that was being communicated.

That's how mathematics notation is developed. The geometry, or whatever is being analysed, is primary to the language

 

[chrisr999]

you see, jgens,
calculus examines CURVES using STRAIGHT LINES.

The "infinitesimals", which is a term i haven't used until this discussion!, go hand in hand with the "limits".

You can't have rain without water, they are the same thing.
We are comfortable with straight lines.

Geometrically, calculus uses straight lines to handle curves and in order to be exact, not just "roughly accurate", the length of those straight lines go to zero!
The trickyness of the math handles this vanishing act!

sounds really contradictory, but it's pretty clever. these mathematicians were good.
It sounds more complicated than it is, it just takes getting used to, but without your mental microscope, it may not seem so clear

 

[jgens]

Again, I understand the derivative geometrically! What I'm saying is that a geometric picture means nothing in terms of proof nor does it mean anything in terms of the derivative as a fraction. If you want to work with differentials as jambaugh suggested or non-standard calculus as both HallsofIvy and I mentioned then there is nothing wrong with saying the derivative is a ratio of dy to dx.

If however, you're working within the real number system, the notion of the derivative as a ratio of two infinitessimals is non-sensical because infinitessimals do not exist as a subset of the real numbers.

Proof: For definiteness, suppose k is a positive infinitessimal, then k must satisy,

0 < k < 1/n ∀n ∈ N

This clearly defines a sequence. Letting the sequence {x_n} = 1/n we can show that this sequence is convergent to zero using the definition of convergence.

(∀ε)(ε > 0)(∃N)(∀n)(if n > N then 0 < |x_n - 0| < ε)

If ε > 0, then clearly for some N ∈ N, 0 < 1/N < ε. However, if n > N then x_n = 1/n < 1/N < ε, hence, 0 < |x_n - 0| < ε.

Consequently, 0 < k < 0 and by the Squeeze Theorem, k = 0. Q.E.D.

We've argued this point ad nauseum!

 

[chrisr999]

You're getting too deep into definitions and "ways of description", jgens.
Sincerity to understand will unravel it for you very simply.
Keep trying, no-one's arguing about anything!
Look simply and you will see that the maths in the situation you are trying to understand has a geometric or "point co-ordinate" foundation to it!
Sometimes previous knowledge can get in the way of seeing something and no-one's co-ercing you to adopt their point of view!
Only, "have a look at this, do you see what i see?"

 

[chrisr999]

If you refer back to my .pdf diagram,
are you seeing the ratio of the "infinitesimals" or the ratio of "dy" to "dx" at the point "t" as being EXACTLY equal to the ratio of the 3 triangles on the left side of the tangent to the graph at "t"?
Check if this is clear first.
Remember, you cannot see the infinitesimals at the limit, but the overlapping triangles show you what's happening to the "infinitesimals".
I'm referring to the "infinitesimals" as the perpendicular sides of the triangle that is imploding as the "crude gradient" line is being tilted to reach the tangent.
Because the triangles to the right are disappearing.
Therefore the tangent reveals the ratio of the infinitesimals.
Using the tangent, you don't even have to bother with infinitesimals!
But if you can "see" this, you'll see the whole picture of what happens at the limits and not just a part of it.
Notice that textbooks tend to concentrate on one description or another.
I've encapsulated the entire story of a derivative, meaning the "instantaneous rate of change" of the graph with this picture.
I designed it today, it's not from any textbook, then i made a .pdf file.

Persist and if you go beyond the frustration of trying to understand, it will reveal it's intricacy to you, maybe subconsciously at first but it will become clear unless you cut off your enquiry.

 

[chrisr999]

Try to imagine the triangle that's touching the graph at "c" and "t" getting smaller and smaller as "c" moves to "t".
It's disappearing but the limit of the ratio of it's perpendicular sides, as "c" continues on to "t" is the ratio of the perpendicular sides of any of the triangles at the left of the tangent.
This is what's happening.
To understand it all, you only need appreciate the following...

Why start at "a"?
Why move "a" to "t"?
Why start the maths using the gradient of a straight line?
Why approach a limit?
Why is the ratio of the sides of the disappearing triangle equal to the ratio of the 3 lined up on the tangent?

Imagine the point "a" moving to "t" and imagine what the triangle "looks like" as "a" hits "t".

There is no triangle right! at least there shouldn't be. not quite!
mathematically, if you are driving your car, you are actually traveling at an instantaneous speed at an instant in time, of course that instant has no time interval!

You see in school, students are taught to work with averages, then move on to calculus and at best many can perform the techniques without grasping the intricacy of calculating with an interval of zero,
you see the same in integration.
Don't get trapped in the definitions of limits, derivatives, differentials, infinitesimals, real numbers etc, otherwise you're getting into "humpty dumpty" territory. Try to get the "story" of it. That's what mathematicians have to do.
If someone hires you to get an "A" for their "D" level student, you don't use the same teaching materials that got them a "D".

How long is the moment we live in?
it can't be measured.
You can only measure an "interval"

What's the probability of being a height or age if that height or age is a real value?
you can't measure it, hence we use probability distributions and analyse intervals instead.

 

[Hurkyl]

There is no triangle right! at least there shouldn't be. not quite!

Then why do you tell them there is? From your PDF:

Hence the right-angled triangle we were using to write the line gradient (between 2 points on the curve) has DISAPPEARED! or has it??
Consider this to have become reduced to the molecular level ... Now imagine magnifying this until it’s clearly visible again ... Once the limit as \Delta x \rightarrow 0 has been evaluated, \frac{dy}{dx} = \frac{\Delta y}{\Delta x} for the tangent.​

Things like this are the reason you are being criticized. You seem to know full well that there isn't a triangle. But you tell them it really is still there, and really small. Even worse, the way you talk about the limit of \frac{\Delta y}{\Delta x} as if we were simply plugging the value "\Delta x \rightarrow 0". Yes, I know that doesn't make sense, but the students don't know that.

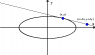
What makes this sad it would take very little to turn this into a series of actual, true statements that don't require magnifying mythical hypotenuses of zero length or infinitessimals or anything like that. You want to talk about scaled triangles? Then do that. Draw a circle Z around t and mark the point L where the tangent line at t intersects Z. Then mark the points where the segments ta, tb, tc intersect Z and demonstrate how that intersection approaches L.

And emphasize that it's approaching -- don't phrase things as if the tangent line is really just another secant line.

(Maybe you'd prefer using a vertical line segment at x_t+1 instead of the circle, so you can work more nicely with right-triangles. The circle is nice because it doesn't depend on a choice of coordinates and handles vertical tangents easily, but the line is nice because it 'measures' slope rather than angle and is simpler algebraically)

You see in school, students are taught to work with averages, then move on to calculus and at best many can perform the techniques without grasping the intricacy of calculating with an interval of zero,

You make it sound like calculus is just a clever way to divide by zero without error.

Try to get the "story" of it. That's what mathematicians have to do.

You're missing the point. Yes, the story is important. But it's hard to convey the story if you leave stuff out and don't tell the rest right. At this point, I'm not even sure if you have a well-defined story to tell!

e.g. what do you think a "triangle reduced to the molecular level" is?

 

[OrderOfThings]

I'm curious what you think "d^2 f/dx^2" means (along with "d^2 x") -- when I learned calculus, that literally meant "the second derivative of f with respect to x then x"

Take a curve in the x,y-plane and pick a tangent vector field along the curve. Then at a point (x,y), the tangent vector has coordinates (dx,dy) and the derivative of the tangent vector has coordinates (d^2x,d^2y). The derivative of y as a function of x can be calculated as

\frac{dy}{dx}

and the second derivative is

\frac{d}{dx}\left(\frac{dy}{dx}\right)=\frac{d^2y\,dx-dy\,d^2x}{dx^3}.

If the curve is parametrized by a multiple of x, then dx=\textrm{const} and d^2x=0 and the second derivative formula reduces to

\frac{d^2y}{dx^2}.

For any affine reparametrization u=ax+b, then also d^2u=0 and

\frac{d^2y}{dx^2}\cdot\left(\frac{dx}{du}\right)^2=\frac{d^2y}{du^2}.

 

[jambaugh]

jambaugh, is it possible to rigorously develop calculus using differentials? I thought that they were more a calculational trick than anything else, but perhaps not?

Let the coordinates (x,y) represent a point on a smooth curve.
Draw a line tangent to the curve at this point.
Now define a point on this tangent line with coordinates (x+dx,y+dy)

The differentials dx and dy are new variables (not necessarily infinitesimal) which express the coordinates of a point on this tangent line in a coordinate system parallel to the original but with origin (x,y).

Since in this construction the tangent line goes through this translated origin point (x,y),
its equation is dy = m dx + 0, i.e. by definition dy/dx = m = the slope of the tangent line.

This extends to arbitrary dimensions via tangent hyper-planes to hyper-surfaces.

Ultimately we define differentials as coordinates in the tangent space at some point on a manifold. Equivalently they are a basis for the co-tangent space.

 

[jambaugh]

Followup note:
Once we define differentials we can then define the differential operator d.

We understand differentials of variables as new variables with the caveat that constraints on the original variables imply specific constraints on the differential variables. For example:
z\doteq f(x,y) \to dz \doteq \frac{\partial f}{\partial y} dy + \frac{\partial f}{\partial x}dx

Remembering that differentials are variables we may then apply differentials to differentials:
d^2 x,\quad d^3 y,\quad ...

Then given y = y(x) (using y both as the function name and the variable name.)
dy = y&#039;(x)dx
d^2 y = d(y&#039;(x)dx) = y&#039;&#039;(x)dxdx + y&#039;(x)d^2 x
If we later say x = x(t) we then have:
d^2 y = y&#039;&#039;(x)x&#039;(t)x&#039;(t) + y&#039;(x) x&#039;&#039;(t)
or we can simply consider:
\frac{d^2 y}{dx^2} = y&#039;&#039; (x) + y&#039;(x)\frac{d^2 x}{dx^2}
We go back to the geometric definition to see that:
\frac{d^2 x}{dx^2} = \frac{d}{dx}\frac{d}{dx} x + \frac{d}{dx}1 = 0
thence the notation is consistent with the Leibniz notation for the second derivative:
\frac{d^2 y}{dx^2} \doteq y&#039;&#039;(x)

There is a very subtle bit of math here, what's going on is that the decision to allow x to be the independent variable [/i](and to allow the Leibniz notation for second derivative correspond to the literal interpretation of the fraction)[/i] imposes the constraint that its second differential be zero. This is a constraint identity not a definitional identity. One can get into serious trouble by changing around the independent variables and forgetting to "unconstrain" this condition.

Possibly a "better" notation for the second ordinary derivative would be:
y&#039;&#039;(x) = \frac{\partial^2 (d^2 y)}{\partial (dx) \partial (dx)}
But this gets silly and just passes the issue on to the partial derivative notation.

I recommend not using higher order differential notation until one is very very well practiced. I've made embarrassing mistakes trying a cold "derivation" in class using the higher order notation and since stopped. But the Leibniz notation taken as notation is fine and has the virtue of showing the relationship of the units in physical applications.

 

[chrisr999]

I will answer your three questions, Hurkyl,
but please try to think it through.

I said "there is no triangle" at the point of tangency.
Can you see one?
The point of tangency is a "point" and you know what the definition of a point is,
it's a place of zero size.

If a student got to wondering about the apparently contradictory statement of there being a triangle at a point where logically there cannot be one, they will develop the skill to find calculus extremely easy.

It's not a very difficult riddle to resolve.

As I mentioned, the contradiction arises in attempting to write the gradient of the tangent to the graph.
We know the derivative is the gradient of the tangent and "unfortunately" the tangent intersects the curve only at a single point, hence there is no direct way from the function equation to express the gradient.

This is why we start by writing an approximation using two points on the curve itself, which initially is an inaccurate answer.

The overlapping triangles on the right of the tangent that I drew are vanishing as we move to the point of tangency. At the point of tangency we "appear" to have lost that triangle due to the mathematical definition of what a point is or a real number.

Had we not gone this route (though it's a necessary one to formulate the math), we could say it does not matter what size triangle we use against the tangent, since the ratio of the perpendicular sides is constant.

It's the same as looking at something close to you, say a bird for instance.
Now that bird flies away to a remote location. On it's path, there comes a point where you can no longer see it, even if we didn't have the horizon to contend with, but that doesn't mean it's not there.
At the point of tangency, according to the definition of real numbers, there can be no triangle there, but such definitions only mask the truth of the situation.

I chose to illustrate in that manner to encourage the student to exercise his imagination and resolve the apparent contradiction and not get tangled up in definitions where those definitions become a barrier.

The triangles on the left of the tangent help resolve the confusion as the student can easily imagine this shape reducing in size ad infinitum WITHOUT EVER DISAPPEARING COMPLETELY, even though the ones on the right do "appear to be disappearing", though approaching a limit which is still worded in a regimental way.

To answer the "divide by zero" question... Did you not see in the .pdf file that i said "We are not actually dividing by zero at all"?

That problem is resolved again by examining both types of triangle on both sides of the tangent.

Remember 2x/x is always 2 no matter how small x is but if you say 2x is zero as x goes to zero and x is zero as x goes to zero, so 2x/x is 0/0 as x goes to zero means we've gone a step too far and have forgotten to keep an eye on what the ratio is.

Use your creativity to try the 3rd question,
I guarantee you, a student can improve rapidly when you ask them to be imaginative.
I've gotten students to improve by 3 grades in a few lessons, where they had been floundering within the established educational system.

 

[Hurkyl]

Take a curve in the x,y-plane and pick a tangent vector field along the curve Then at a point (x,y), the tangent vector has coordinates (dx,dy) and the derivative of the tangent vector has coordinates (d^2x,d^2y).

So... you have in mind having some implicit parametrization of the curve (which I will call s) and when you say "dx", what you really mean is "the derivative of x with respect to s", and similarly "d²x" is shorthand for "the second derivative of x with respect to s".

If you actually write that out in Leibniz notation rather than using shorthand, what you mean by d²y / dx² is

\frac{\frac{d^2y}{ds^2}}{\left( \frac{dx}{ds} \right)^2}

is that correct?

The problem is that this doesn't mesh with how people actually use Leibniz notation. The specific counterexample I had in mind when I wrote my post could be formulated as

x=s³
y=x³

and (AFAIK) most people would expect to have

\frac{d^2y}{dx^2} = 6x

whereas your interpretation would result in 8x.

One specific case where this might arise (and where I've seen trip up even knowledgeable people) is doing a change-of-variable for second derivatives. (edit: ah, I see jambaugh pointed that out already)

 

[OrderOfThings]

So... you have in mind having some implicit parametrization of the curve (which I will call s) and when you say "dx", what you really mean is "the derivative of x with respect to s", and similarly "d²x" is shorthand for "the second derivative of x with respect to s".

If you actually write that out in Leibniz notation rather than using shorthand, what you mean by d²y / dx² is

\frac{\frac{d^2y}{ds^2}}{\left( \frac{dx}{ds} \right)^2}

is that correct?

Well yes, since ds=1, the above fraction is identical to the fraction d^2y/dx^2. This is not a shorthand notation. But this fraction is only equal to the second derivative of y as a function of x when d^2x=0.

The problem is that this doesn't mesh with how people actually use Leibniz notation. The specific counterexample I had in mind when I wrote my post could be formulated as

x=s³
y=x³

and (AFAIK) most people would expect to have

\frac{d^2y}{dx^2} = 6x

whereas your interpretation would result in 8x.

The second derivative is computed by

y&#039;&#039;(x) = \frac{d}{dx}\left(\frac{dy}{dx}\right) = \frac{d^2y\,dx-dy\,d^2x}{dx^3} = 6x.

Nothing wrong here I think.

 

[Hurkyl]

I said "there is no triangle" at the point of tangency.

Yes, you did say "the triangle ... has DISAPPEARED" -- which you immediately deny it by saying "or has it?", followed shortly by "it's really still there".

What exactly is the "story" do you want the students to see? Use a definition if you have to -- precisely conveying ideas is one of the things those are really good at.

 

[chrisr999]

you see, the way you are wording your question when you say..."I say the triangle has disappeared" and then I say "or has it",

this is just a way to ask the student to hold on for a second and wonder about what's really happening,
encouraging them to think it through,
or rather, to be more precise, to ask them if they can begin to imagine what is happening to both the triangle that is "changing shape" and the one that can be drawn at any size you like.

True, if the student has trouble imagining it, I can develop an animation for them, but only if their visual modality is not very active.

the mathematics of calculus is easy to understand non-verbally, without reference to number systems or notation of any kind. Bear in mind, to write a book or speak we must use some kind of symbols.
Also, when you are driving along in your car at various instantaneous speeds, you do not need any diagrams or notation, you only need your senses.

Now, the triangle that is "changing shape", the one from which we write the gradient of the line using 2 points on the curve itself (the crude gradient) is the one that is "disappearing", "appearing to disappear", "imploding", "approaching a galactic black hole" or however we want to illustrate it's vanishing act, will of course cause trouble for students that have become "notationally dependent".
They try math by working "in the dark" so to speak and end up in trouble with the description.
it is not the description that is important to understand but THE DESCRIBED". There are numerous ways to describe the described.

Bringing up the topic of the vanishing triangle, which is at the heart of the conflicting views regarding "dividing by zero", "limit of fractions", "limits" etc which are all incomplete ways to approach the problem, introduces the problem that is a side-effect of the "notation".

So you examine all of that, you don't give up the analysis but continue on because someone points out that "the problem of the vanishing triangle is resolved by the gradient of the tangent itself".
This is a visual comprehension, whereby the student is asked to imagine reducing it to as small a size as possible and compare it to the the smallest size they can imagine for the vanishing triangle.
It's not really all that Lazarus-like.

If you never got into notation at all, you could simply say, the function derivative is always the gradient of the tangent that you can move all around the curve. Of course that would not be mathematically efficient!

However it does offer instantaneous comprehension from which you can write the understanding in numerous ways, hopefully while being aware of the confusion introduced by choosing only one of the notational modalities available.

 

[chrisr999]

I will write up the story as an attachment, am a little busy at the moment