- #1
Menaus
- 54
- 0
Prove that in any triangle, if the angle bisectors of two angles are congruent, then the triangle is isosceles
Before I give my proof, here is a lemma to it:
If a pair of vertical angles both have angle bisectors, then all resulting angles are congruent.

Given: Vertical Angles [itex]∠2[/itex] and [itex]∠4,[/itex] and [itex]∠1[/itex] and [itex]∠3,[/itex] Angle bisectors such that [itex]∠1 \cong ∠2[/itex], and [itex]∠3 \cong ∠4[/itex]
By vertical angle theorem, ∠1 and ∠3 must be congruent, as well as ∠2 and ∠4.
∠3 and ∠4, must be congruent, ∠1 and ∠2 must also be congruent by the definition of angle bisector.
By the transitive property of congruent angles theorem, ∠1 and ∠4 must be congruent, and ∠2 and ∠3 must also be congruent.Therefor, all angles must be congruent to each other.This concludes the lemma, here is my proof. Please poof read it... No pun intended. ;)In any triangle, if the angle bisectors of two angles are congruent, then the triangle is isosceles
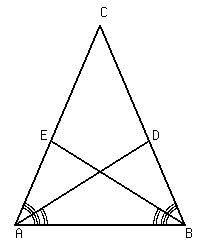
Given: [itex]ΔABC, ∠EAD\cong∠EAB, ∠DBE\cong∠DBA,[/itex] and [itex]AD = BE[/itex]
Let there exist a line through FO (where O is the point in which AD, and BE intersect) such that line FO is congruent to segment AB
Let there exist a point G where line GB is perpendicular to segment AB.(Please note, for the purposes of this proof, there need not be a line perpendicular to segment AB, I am simply trying to show where G is, in relation to all other parts of the diagram)
∠AOF, ∠FOE, ∠BOG, and ∠GOD are all congruent to each other by my lemma, I'll call it the Vertical ∠ Bisector Theorem.
∠OBA is congruent to ∠FOE by PAI theorem.
∠GOD is congruent to ∠AOF by PAI theorem
By the transitive law of congruent angles, ∠OBA and ∠OAB are congruent
By the transitive law of congruent angles, ∠CAB, and ∠CBA are congruent
Congruent angles imply congruent segments, therefor, AC = BC
quod erat demonstrandumIs my proof correct? Do I need to be more rigorous? What problems are there?
Before I give my proof, here is a lemma to it:
If a pair of vertical angles both have angle bisectors, then all resulting angles are congruent.
Given: Vertical Angles [itex]∠2[/itex] and [itex]∠4,[/itex] and [itex]∠1[/itex] and [itex]∠3,[/itex] Angle bisectors such that [itex]∠1 \cong ∠2[/itex], and [itex]∠3 \cong ∠4[/itex]
By vertical angle theorem, ∠1 and ∠3 must be congruent, as well as ∠2 and ∠4.
∠3 and ∠4, must be congruent, ∠1 and ∠2 must also be congruent by the definition of angle bisector.
By the transitive property of congruent angles theorem, ∠1 and ∠4 must be congruent, and ∠2 and ∠3 must also be congruent.Therefor, all angles must be congruent to each other.This concludes the lemma, here is my proof. Please poof read it... No pun intended. ;)In any triangle, if the angle bisectors of two angles are congruent, then the triangle is isosceles
Given: [itex]ΔABC, ∠EAD\cong∠EAB, ∠DBE\cong∠DBA,[/itex] and [itex]AD = BE[/itex]
Let there exist a line through FO (where O is the point in which AD, and BE intersect) such that line FO is congruent to segment AB
Let there exist a point G where line GB is perpendicular to segment AB.(Please note, for the purposes of this proof, there need not be a line perpendicular to segment AB, I am simply trying to show where G is, in relation to all other parts of the diagram)
∠AOF, ∠FOE, ∠BOG, and ∠GOD are all congruent to each other by my lemma, I'll call it the Vertical ∠ Bisector Theorem.
∠OBA is congruent to ∠FOE by PAI theorem.
∠GOD is congruent to ∠AOF by PAI theorem
By the transitive law of congruent angles, ∠OBA and ∠OAB are congruent
By the transitive law of congruent angles, ∠CAB, and ∠CBA are congruent
Congruent angles imply congruent segments, therefor, AC = BC
quod erat demonstrandumIs my proof correct? Do I need to be more rigorous? What problems are there?
Last edited:
 ]
]