Amplitude of oscillation of a mass which is the pivot of a pendulum

[lorenz0]

Homework Statement

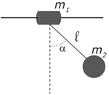
Two bodies (see figure) are connected by an ideal rope of length $l = 0.9 m$. The body with mass $m_1 = 2 kg$ is free to slide without friction along a rigid horizontal rod. The second body has mass $m_2 = 3 kg$. The bodies are both initially stationary in the indicated position ($\alpha = 60 °$) when they are left free to move. Find:
a) the velocities $v_1$ and $v_2$ of the two bodies when they are vertically aligned;
b) the amplitude $A$ of the motion of $m_1$.

Relevant Equations

$U_g=mgh, E_i=E_f, E=U+K, P_i=P_f$

1) By conservation of mechanical energy we have $m_2gl(1-\cos(\alpha))+m_1gl=\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2+m_1gl$ and by conservation of linear momentum along the x-axis we have $m_1v_1+m_2v_2=0$ which gives us $v_2=\sqrt{\frac{2m_1gl(1-\cos(\theta))}{m_1+m_2}}$ and $v_1=-\frac{m_2}{m_1}v_2$

2) For $m_2$ I think that the amplitude should be $A_2=2l\sin(\alpha)$ but I don't see how find out the amplitude of $m_1$ so I would appreciate an hint about how to find it, thanks.

 

[haruspex]

2) For $m_2$ I think that the amplitude should be $A_2=2l\sin(\alpha)$

Wouldn't that be the amplitude relative to $m_1$?
Where is the mass centre when the rope is vertical?

 

[lorenz0]

Wouldn't that be the amplitude relative to $m_1$?

yes, and my problem is that I don't see how I can go from that to the "general" amplitude of $m_1$

 

[lorenz0]

Wouldn't that be the amplitude relative to $m_1$?
Where is the mass centre when the rope is vertical?

vertically along the rope, at position $\frac{m_1}{m_1+m_2}\cdot l$ wrt mass $m_2$ or at position $\frac{m_2}{m_1+m_2}\cdot l$ with respect to $m_1$. Perhaps since there are no horizontal external forces the x-position of the CM is constant

 

[lorenz0]

Wouldn't that be the amplitude relative to $m_1$?
Where is the mass centre when the rope is vertical?

By imposing that the x-position of the center of mass (calculated wrt a frame centered on $m_1$) is constant I get that the amplitude of the motion of $m_1$ is $\frac{m_2}{m_1+m_2}l\sin(\alpha)=A$ but according to the text I am using it should be twice as much. Any thoughts?

 

[TSny]

By imposing that the x-position of the center of mass (calculated wrt a frame centered on $m_1$) is constant I get that the amplitude of the motion of $m_1$ is $\frac{m_2}{m_1+m_2}l\sin(\alpha)=A$ but according to the text I am using it should be twice as much. Any thoughts?

This looks correct to me. Perhaps the text is using "amplitude" to mean the total distance between the left and right turning points of $m_1$. Your interpretation is the same as what I would have assumed.