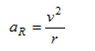An object is launched from the Earth to escape the Sun

In summary, the escape velocity from the Sun for an object in Earth's orbit (of orbital radius R) but far from the Earth is v = (G*M(sun)/R)^1/2 = 29.8 km/s. To escape from the Sun, an object with a speed equal to the Earth's orbital speed must be given an additional speed of 12.3 km/s. For an object launched from Earth in the direction of Earth's orbital motion, it must be given a launch speed v so that when it is far from Earth, but still at a distance of about R from the Sun, it has an additional speed of 12.3 km/s and can escape from the Sun. This can be found by
  • #1
bobbsmmith
3
1

Homework Statement


(a) What is the escape speed from the sun for an object in the Earth's orbit (of orbital radius R) but
far from the Earth? (b) If an object already has a speed equal to the Earth's orbital speed, what
additional speed must it be given to escape as in (a)? (c) Suppose an object is launched from Earth
in the direction of the Earth's orbital motion. What speed must it be given during the launch so
that when it is far from Earth, but still at a distance of about R from the sun, it has that additional
speed calculated in (b) and thus can escape from the sun?
upload_2017-12-2_18-32-22.png

Homework Equations


upload_2017-12-2_18-33-8.png

upload_2017-12-2_18-35-22.png


F = ma

The Attempt at a Solution


I was able to find the answers for parts (a) and (b), but am completely unsure of where to go for part (c). At first, I thought that I needed to find the distance away from the Earth at which the object has a speed of 12.3 km/s (obtained from part (b)), and then use that distance to calculate the velocity of launch. When I did that, I just ended up with the Earth's orbital speed, as calculated in part (b).

1. F = ma = mv^2/R = G * M(sun) * m/R^2
2. v = (G*M(sun)/R)^1/2 = 29.8 km/s

Once I did that, I realized I must not be on the right track. I'm completely unsure of where to begin!
 

Attachments

  • upload_2017-12-2_18-32-22.png
    upload_2017-12-2_18-32-22.png
    7.9 KB · Views: 319
  • upload_2017-12-2_18-33-8.png
    upload_2017-12-2_18-33-8.png
    5.5 KB · Views: 316
  • upload_2017-12-2_18-35-22.png
    upload_2017-12-2_18-35-22.png
    1.4 KB · Views: 322
  • Like
Likes berkeman
Physics news on Phys.org
  • #2
The Sun is irrelevant for part (c) (apart from using the result from (b)) as you only consider the motion close to Earth. If you launch an object with speed v from the surface of Earth, what is its speed far away from Earth?
 
  • #3
mfb said:
The Sun is irrelevant for part (c) (apart from using the result from (b)) as you only consider the motion close to Earth. If you launch an object with speed v from the surface of Earth, what is its speed far away from Earth?
Would it be v = sqrt(G*M(earth)/R) where R is the distance between the center of the Earth and the object?
 
  • #4
That is related to (but not equal to) the escape velocity, the minimal velocity to get it away from Earth. But then it has "zero velocity" far away from Earth, not the 12.3 km/s it needs to escape from the Sun.

It is also not an answer to my question, which should be a velocity as function of the unknown v.
 
  • #5
mfb said:
That is related to (but not equal to) the escape velocity, the minimal velocity to get it away from Earth. But then it has "zero velocity" far away from Earth, not the 12.3 km/s it needs to escape from the Sun.

It is also not an answer to my question, which should be a velocity as function of the unknown v.
Then I'm just not sure of what its speed far away from Earth would be.
 
  • #6
Think of how the escape velocity is derived. Which conservation law is used?
 

1. What is meant by "escaping the Sun"?

"Escaping the Sun" refers to an object reaching a point in its orbit where it is no longer under the gravitational influence of the Sun. This means the object will continue to travel through space in a straight line, rather than being pulled towards the Sun.

2. How is an object launched from the Earth to escape the Sun?

To launch an object from the Earth to escape the Sun, a spacecraft must travel at a speed of approximately 42.1 km/s. This is known as the "escape velocity" and allows the spacecraft to overcome the gravitational pull of the Sun.

3. What factors affect an object's ability to escape the Sun?

The main factors that affect an object's ability to escape the Sun are its mass and its distance from the Sun. The greater the mass of the object, the more energy is needed to escape the Sun's gravitational pull. Similarly, the closer an object is to the Sun, the stronger the gravitational pull and the more energy is needed to escape.

4. Can any object be launched from the Earth to escape the Sun?

Yes, any object can be launched from the Earth to escape the Sun as long as it has enough energy to reach the escape velocity. However, it is much easier for smaller and lighter objects to achieve this velocity compared to larger and heavier objects.

5. What happens to an object after it escapes the Sun?

Once an object escapes the Sun, it will continue to travel through space in a straight line at a constant speed. It may encounter other objects or gravitational forces that alter its trajectory, but it will no longer be orbiting the Sun.

Similar threads

Rocket Escape Velocity from the Earth-Sun system
    • Introductory Physics Homework Help
Replies
3
Views
1K
Calculating distance of Mars from the Sun based on two elongations
    • Introductory Physics Homework Help
Replies
2
Views
606
Orbital speed variation as a planet orbits the Sun
    • Introductory Physics Homework Help
Replies
5
Views
934
Finding r of a Jovian-synchronous orbit and escape velocity
    • Introductory Physics Homework Help
Replies
7
Views
1K
Gravitational PE for a certain distance from the Sun
    • Introductory Physics Homework Help
Replies
8
Views
732
Different sunset times due to elevation ##h## at a point on the Earth
    • Introductory Physics Homework Help
Replies
13
Views
492
Earth's Acceleration Toward the Sun
    • Introductory Physics Homework Help
Replies
5
Views
6K
Moment of Inertia of a sphere about an axis
    • Introductory Physics Homework Help
Replies
4
Views
1K
What is the distance between the Sun and the Earth?
    • Introductory Physics Homework Help
Replies
18
Views
2K
Opacity and density of the sun
    • Introductory Physics Homework Help
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top