Analysing a double capacitor circuit with no battery

[Felipe Lincoln]

Problem: At the instant $t=0$ the capacitor C1 has a charge $Q_0>0$ and the capacitor C2 has no charge. (I forgot to draw the switch to close and open the circuit), so the switch is closed and the current start flowing. Let the circuit goes to $t\to\infty$. a) What's the energy stored in each capacitor? b) How does the current vary over time? c) What's the power dissipated in each resistor at an instante $t>0$ ?

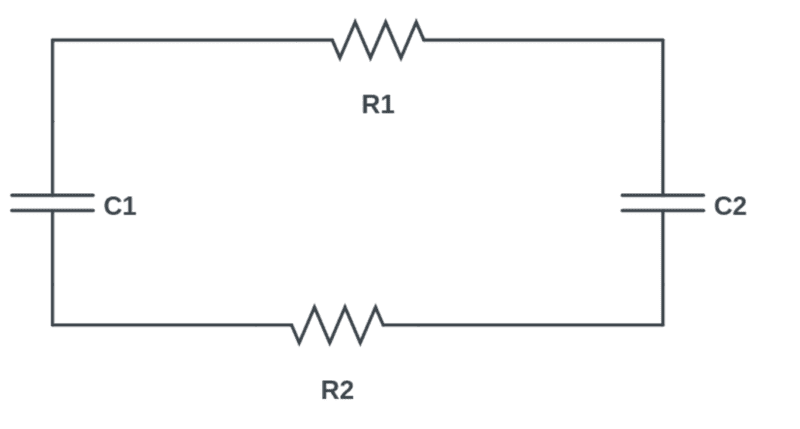
How I'm trying: The energy in each capacitor would be $\frac{1}{2}CV_F^2$ and this $V_F$ will be the same in both capacitor because there will be no current flowing once there's no moving charge. Ok, but how can I find this $V_F$? I had no success on trying kirchhoff mesh law because I ended with two function of charge over time and couldn't solve the differential equation. $$\dfrac{Q_1(t)}{C_1} = (R_1+R_2)i(t) + \dfrac{Q_2(t)}{C_2}$$
Here is where I stopped, can't get any further than this.

 

[berkeman]

Welcome to the PF.

(In the future, please use the Template you are provided when starting a new schoolwork thread. Thank you.)

Are you familiar with the differential equation that relates the current through a capacitor to the voltage across it? I would use that with either KCL or KVL to work toward the solution...

 

[Orodruin]

You need a relation between $Q_1(t)$ and $Q_2(t)$. How do they relate to the current?

 

[Felipe Lincoln]

Are you familiar with the differential equation that relates the current through a capacitor to the voltage across it?

Not really, I'm a bit confused.

You need a relation between $Q_1(t)$ and $Q_2(t)$. How do they relate to the current?

The problem didn't gave me this information, I don't know how I can relate them.

 

[Orodruin]

Not really, I'm a bit confused.

The problem didn't gave me this information, I don't know how I can relate them.

The prolem should not need to.

 

[Felipe Lincoln]

I can relate one with other through the stored energy, but I don't think the energy conserves so I can use $\frac{1}{2}Q_0^2/C_1 = \frac{1}{2}Q_1^2/C_1+\frac{1}{2}Q_2^2/C_2$. Is there another way that I'm missing?

 

[berkeman]

Not really, I'm a bit confused.

Well, then following Orodruin's hints, are you familiar with the differential equation that relates the current through a capacitor to the change in the charge Q on that capacitor?

If not, how have you been doing other calculations on RC circuits up to now?

 

[Felipe Lincoln]

Well, then following Orodruin's hints, are you familiar with the differential equation that relates the current through a capacitor to the change in the charge Q on that capacitor?

If not, how have you been doing other calculations on RC circuits up to now?

Hm.. I just know how to deduce each of them, V, Q and I and how to apply them into a trivial case, battery, resistor and capacitor. This is the first problem out of my preview experiences that I'm facing.

 

[berkeman]

Have you taken any simple calculus? Do these equations look familiar?

i(t) = C \frac{dv(t)}{dt}

i(t) = \frac{dQ(t)}{dt}

 

[Felipe Lincoln]

Yes, I took. And they are familiar. So, the current measured from one capacitor is the same as if I measure from the other, uh? I was thinking in them separately, oh god.

 

[berkeman]

So, the current measured from one capacitor is the same as if I measure from the other, uh?

Yes, and Orodruin's method is probably a little easier than using the equation that I first suggested. So you have the same current flowing around the whole circuit, which discharges one capacitor and charges the other until they reach the same voltage, when the current decays to zero. Can you try working with that?

 

[Felipe Lincoln]

Sure! Let me see:
For the capacitor 2 we have a current:
$$ i(t) = C_2\dfrac{\mathrm{d}v_2(t)}{\mathrm{d}t} = C_2\dfrac{\mathrm{d}}{\mathrm{d}t}\left[ v_f(1-\mathrm{e}^{-t/RC_2})\right] = C_2\dfrac{v_f}{RC_2}\mathrm{e}^{-t/RC_2} = \dfrac{Q_f}{RC_2}\mathrm{e}^{-t/RC_2} $$
Being $v_f$ and $Q_f$ the voltage and charge this capacitor will have.
For the capacitor 1.
$$ \dfrac{\mathrm{d}Q_1(t)}{\mathrm{d}t} = \dfrac{\mathrm{d}}{\mathrm{d}t}\left[ Q_0\mathrm{e}^{-t/RC_1}\right] = -\dfrac{Q_0}{RC_1}\mathrm{e}^{-t/RC_1}$$
Now
$$ \dfrac{Q_f}{RC_2}\mathrm{e}^{-t/RC_2} = -\dfrac{Q_0}{RC_1}\mathrm{e}^{-t/RC_1}$$
$$ \dfrac{Q_f}{C_2}\mathrm{e}^{1/C_2} = -\dfrac{Q_0}{C_1}\mathrm{e}^{1/C_1}$$
$$ Q_f= -Q_0\dfrac{C_2}{C_1}\mathrm{e}^{C_2/C_1}$$

Is it right?
I have some basic questions.. What resistance should I consider when I'm writing my RC equations? The equivalent resistance between the capacitor terminals? And another even more fundamental, by the equations above, I see that the final charge in the capacitor 2 doesn't depends on the resistance of the circuit, which means that it conserves, I have the idea that if I lost energy on the resistor I'm losing charge, why is it not true?

 

[berkeman]

What resistance should I consider when I'm writing my RC equations?

I would just combine the 2 resistors into their series sum. The same current flows through both of them.

I see that the final charge in the capacitor 2 doesn't depends on the resistance of the circuit, which means that it conserves, I have the idea that if I lost energy on the resistor I'm losing charge,

Charge is conserved (there is nowhere else for it to go), but energy is not. This is very similar to the classic problem where you have 2 capacitors, one charged and one not. Then you connect them in parallel. Using Q=CV and the fact that charge is conserved, you can calculate the final voltage in terms of the initial charged cap's voltage. But then you are asked to use those values to calculate the initial and final energies E = 1/2 CV^2, and it turns out to be less than the initial energy.

 

[berkeman]

This is very similar to the classic problem where you have 2 capacitors, one charged and one not. Then you connect them in parallel. Using Q=CV and the fact that charge is conserved, you can calculate the final voltage in terms of the initial charged cap's voltage. But then you are asked to use those values to calculate the initial and final energies E = 1/2 CV^2, and it turns out to be less than the initial energy.

http://www.users.on.net/~ithilien/tam/electronics/CapacitorParadox.html

 

[Felipe Lincoln]

I'll read it, thanks for sharing your knowledge, and thank you too Orodruin,