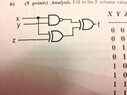shamieh
- 538
- 0
Fill in the F column values in the truth table for the circuit.
Need someone to check my work.
View attachment 1444
My Answer:
Need someone to check my work.
View attachment 1444
My Answer:
- x y z | f | x! and y! | x! XOR z|
- 0 0 0| 0 | 1 | 1
- 0 0 1| 1 | 1 | 0
- 0 1 0| 1 | 0 | 1
- 0 1 1| 0 | 0 | 0
- 1 0 0| 0 | 0 | 0
- 1 0 1| 1 | 0 | 1
- 1 1 0| 1 | 1 | 0
- 1 1 1| 0 | 1 | 1