- #1
derya
- 2
- 1
- TL;DR Summary
- Seeking the solution of an integral over polar coordinates.
Hi,
I am trying to find open-form solutions to the integrals attached below. Lambda and Eta are positive, known constants, smaller than 10 (if it helps). I would appreciate any help! Thank you!
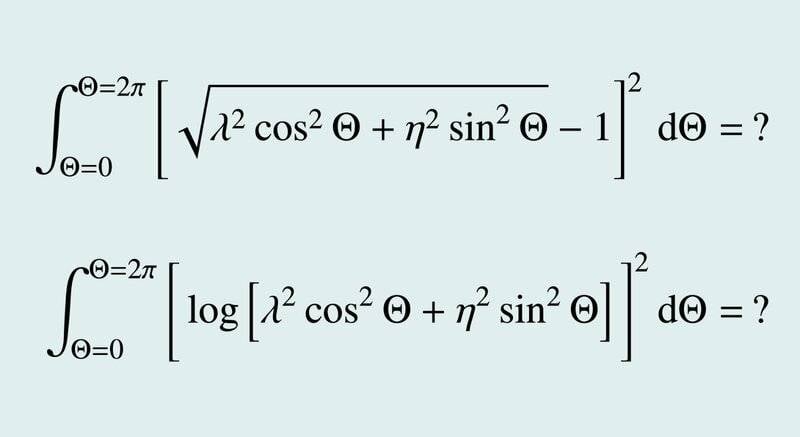
I am trying to find open-form solutions to the integrals attached below. Lambda and Eta are positive, known constants, smaller than 10 (if it helps). I would appreciate any help! Thank you!