Analyzing Shear & Bending on Idealized Cross Section

[greg_rack]

Homework Statement

POINT A)
Calculate the internal shear force and bending moment(no torque) that would cause the internal stress state given above. Clearly indicated both magnitude and direction, and
show/describe how you arrive at this answer. You may assume the internal loads act at the centroid.

POINT B)
Your colleague seems to recall that also an internal torque was present in the original loading of the structure. Indicate whether you agree or disagree with your colleagues recollection.
You do not need to calculate the internal torque, simply identify if it would be zero or non-zero and
provide sufficient reasoning for your decision.

Relevant Equations

Shear flow distribution resulting from applied shear force and torque,
Internal normal stress resulting from internal bending moment

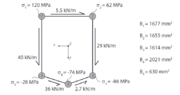
As you can see from the picture, the cross section to analyze is idealized and the boom areas resulting from this are given.
For POINT A) all I did was:

• for determining the shear forces, integrating the shear flows over the sides to compute the vertical and horizontal contribution of each side to the shear forces: sum of vertical contributions will be $V_y$, sum of horizontal $V_x$
• for determining the internal bending moments, calculting MsOI $I_{xx}$ and $I_{yy}$($I_{xy}=0$ because of symmetry) and taking the normal stresses in two booms(e.g., 1 and 2) to solve the system of eqs. below for $M_x$ and $M_y$: $$\left\{\begin{matrix}
  \sigma_1=\frac{M_x}{I_{xx}}y_1+\frac{M_y}{I_{yy}}x_1 \\
  \sigma_2=\frac{M_x}{I_{xx}}y_2+\frac{M_y}{I_{yy}}x_2 \\
  \end{matrix}\right.$$

This gives results for $V_x, \ V_y, \ M_x, \ M_y$
When it comes to POINT B) though, I get quite confused. What I would do is calculating the shear center SC(in this case, reading the statement of POINT A) I am led to think and assume that this coincides with the centroid C of the section even though this is not true in general; what do you think about this?) of the cross section and then take the moment generated by the shear flow distribution around that point: if the resulting moment is zero, then no torque is present; if it differs from zero, then it means that a torque is acting on the cross section.
Would this make sense? If no, what would? If yes, is there any other(smarter) way to answer the question?

 

[Lnewqban]

The shear center location is the key in this problem.

Look for 8.4 in the following link:
https://ocw.snu.ac.kr/sites/default/files/NOTE/7511.pdf

“If the sear forces are not applied at the shear center, the beam will undergo both bending and twisting.”

 

[greg_rack]

The shear center location is the key in this problem.

Look for 8.4 in the following link:
https://ocw.snu.ac.kr/sites/default/files/NOTE/7511.pdf

“If the sear forces are not applied at the shear center, the beam will undergo both bending and twisting.”

Thank you for sharing this! Then here, quoting the problem statement:
"You may assume the internal loads act at the centroid."
Which means we can approximate the SC to be located @ C, as internal loads do not cause twisting by definition... correct?
So in this case, for figuring out whether we could or could not have torsion, we just take moments from the shear distribution about C and see whether they add up to 0 or nah(?)

 

[Lnewqban]

That is how I see it.

 

[greg_rack]

Thank you @Lnewqban for your answer!

Another doubt I have regarding to this is: what if I instead took moments about some point other than the SC?
If we don't have torque in the cross section, does this mean that about any point the moments originating from the shear flow distribution must add up to 0? Or does this hold ONLY when we compute such moments about the SC(again, C in this case)?
I know this might sound trivial but it's actually confusing me quite a lot.

Lastly, still with respect to this problem: the $V_y, \ V_x$ we had calculated, assumed no torque. Right?
So if we would now say a torque actually is present, the shear forces would have to be "reshuffled" and recomputed as also the torque would contribute to the final shear flow distribution