How to calculate Shear Flow distribution through an Annulus

[spggodd]

Homework Statement

My problem is how to calculate the Shear Flow Distribution through this open cross-section.
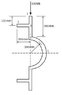
The section has a uniform thickness of 2mm and all other dimensions are on the attached picture.

There is also a 100 kN downwards force applied.

Homework Equations

q(s) = q(s₀) = {(I_xxV_x(z) - I_yxV_x(z)) / (I_yyI_xx - I_xy²)} ∫^s₀tx*ds - {(I_yyV_y(z) - I_yxV_x(z)) / (I_yyI_xx - I_yx²)} ∫^s₀ty*ds

Where the:
I terms are the second moment of areas.
V terms relate to the applied force.
t is the thickness
y is the distance to the overall centroid of the part from the centroid of the sub-section under consideration.
ds is the distance along the sub-section.

For the rectangular sections 1 - 4 I have simplified the equation to:

q(s)=q(s₀)-(V_y(z)/I_xx)∫^s₀ty*ds

The Attempt at a Solution

I have calculated the Second Moment of Area (500.172x10^-6) m⁴
I have calculated all the shears flows up until point 4 on the diagram.
To the left of point 4 is a small rectangular area which I have chosen to neglect, therefore I am concentrating on the Shear Flow around a the remaining quarter annulus which will bring me back to the x-axis.

At point 4 I believe the initial shear stress = 90.168 N/mm based on my workings through the rest of the cross-section up to this point.

I am now stuck at the annulus and I can't seem to find anything in books or my course notes etc..


Thank you for your time.
Steve

 

[SteamKing]

In the annulus, you'll have to squint at the diagram and pretend the thickness of the material is small w.r.t. the radius. You can split the annulus into differential elements where dA = t dθ. You'll have to develop an expression for Q as you go around the annulus, but the shear flow q = VQ/I

 

[spggodd]

Aw man, I had a feeling it was going to be something like that.

Ok I will have a crack at it tomorrow.

Thanks for your help!

 

[spggodd]

Could you offer a link to an reference material?