- #1
Dell
- 590
- 0
for the following cross section
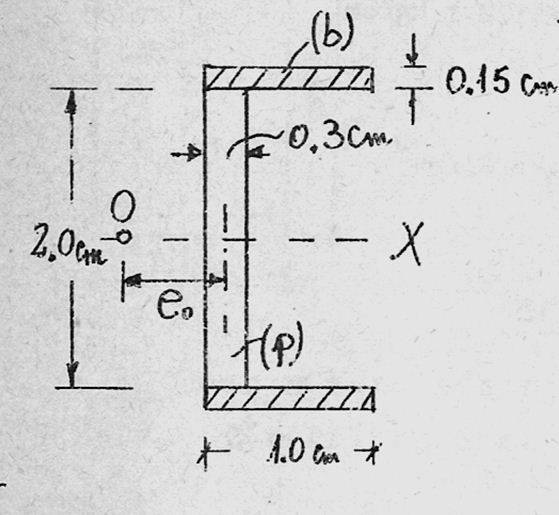
the ratio Eb/Ep=30
find the shear centre of the cross section
-------------------------------------------
first of all i need to find the equivalent cross section, which will be the same except that the horizontal parts will be of length n*L=30*1=30cm
since this cross section has an axis of symmetry, i know that the shear centre passes through that axis, now all i need to find is the distance "eo"
i know that i can move the force to the shear centre and the cross section must feel the same moment, i calculated the moment about a point that passes through the Vertical portion so that only the sums of the horizontal shearing stresses have an effect on the moment,
i know that Q1y is the 1st area moment of each of the horizantal portions,
Q1y=(0.15*s)*1.075 =0.16125*s
I=10.6cm^4
shearing stress=[tex]\int[/tex][tex]\int[/tex](V*Q/I/b)da*2.15 where 2.15 is the distance between the horizontal forces
V*e=[tex]\int[/tex][tex]\int[/tex](V*Q/I/b)da*2.15
e=2.15/(I*0.15)*[tex]\int[/tex]dt[tex]\int[/tex]Qds
e=[2.15/(I*0.15)]*0.15*[tex]\int[/tex](0.16125*s)ds -->from 0 to 30
[2.15/(10.6*0.15)]*0.15*0.16125*302/2=14.7cm
the correct answer is somehow meant to be 0.408cm, can anyone see where i have gone wrong??
the ratio Eb/Ep=30
find the shear centre of the cross section
-------------------------------------------
first of all i need to find the equivalent cross section, which will be the same except that the horizontal parts will be of length n*L=30*1=30cm
since this cross section has an axis of symmetry, i know that the shear centre passes through that axis, now all i need to find is the distance "eo"
i know that i can move the force to the shear centre and the cross section must feel the same moment, i calculated the moment about a point that passes through the Vertical portion so that only the sums of the horizontal shearing stresses have an effect on the moment,
i know that Q1y is the 1st area moment of each of the horizantal portions,
Q1y=(0.15*s)*1.075 =0.16125*s
I=10.6cm^4
shearing stress=[tex]\int[/tex][tex]\int[/tex](V*Q/I/b)da*2.15 where 2.15 is the distance between the horizontal forces
V*e=[tex]\int[/tex][tex]\int[/tex](V*Q/I/b)da*2.15
e=2.15/(I*0.15)*[tex]\int[/tex]dt[tex]\int[/tex]Qds
e=[2.15/(I*0.15)]*0.15*[tex]\int[/tex](0.16125*s)ds -->from 0 to 30
[2.15/(10.6*0.15)]*0.15*0.16125*302/2=14.7cm
the correct answer is somehow meant to be 0.408cm, can anyone see where i have gone wrong??