Angular momentum about a parallel axis O'

[lawsonfurther]

Homework Statement

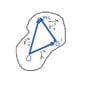
A system has total angular momentum L about an axis O. Show that the system's angular momentum about a parallel axis O' is given by L'=L-h×p, where p is the system's linear momentum and h is a vector from O to O'.

Homework Equations

L=r×p or considering a mass element, L_i=r_i×p_i

The Attempt at a Solution

See picture attached.

It looks like everything makes sense to me except one assumption which is v_i=v'_i. (By the way L is the same as Ltotal in my work)
Or in other words, how do you know that the linear velocity of a mass element relative to an axis when undergoing a circular motion is exactly the same as the one relative to a parallel axis when undergoing another circular motion?
Is there any underlying assumption in this question which has not been pointing out?

 

[TSny]

Welcome to PF.

Linear velocity of a particle in a given frame of reference is independent of the origin that you choose for calculating the angular momentum of the system. When you switch origins from O to O', you are not changing the reference frame for defining linear velocity. There is no need to distinguish between $\vec v_i$ and $\vec v'_i$.

Note that the position vector of the i^th particle relative to O and the position vector of the particle relative to O' are related by $\vec r_i = \vec r '_i + \vec h$. Take the time derivative of both sides.

EDIT: Note that angular momentum of a system of particles is calculated relative to a point, not relative to an axis. I think that maybe you are assuming that angular momentum about an axis implies that the particles are moving in circles about that axis. But, that is not necessarily true. The particles can be moving randomly. Switching from O to O' has no affect on the linear velocities of the particles.

 

[lawsonfurther]

Right. I am assuming that the particles are moving in circles about that axis because the question exactly says that "A system has total angular momentum L about an axis O". Maybe the question is a bit confusing.
But I still didn't get that. I agree that when a system of particles is moving in a straight line, the linear momentum of that system is indeed independent of the origin you choose. But I can't quite imagine the scenario where the statement is also true when the system is undergoing a circular motion. I mean, (at least) assuming it is undergoing a uniform circular motion, the velocity vectors are both perpendicular to their position vectors, which is clearly shown in the picture that the velocity vectors are not the same. How could that be the case?

 

[TSny]

The use of the word "axis" in the problem is confusing to me. Generally, the equation $\sum \vec r_i \times m_i \vec v_i$ is the angular momentum of a system about a point O where $\vec r_i$ is the position of the i^th particle relative to O. Then, when you calculate the angular momentum of the same system relative to another point O', you get the result stated in the problem. Changing from O to O' does not change the velocity of any of the particles.

See bottom of page 15 here:
http://web.mit.edu/8.01t/www/materials/modules/chapter19.pdf
You can see that the calculation here is essentially the same as yours (without any change in velocities of the particles when switching origins).

If you have an object revolving about an axis and if the mass distribution of the object is symmetrical about the axis, then the angular momentum of the object is the same for any origin that lies on the axis of rotation. Then you hear people talk about the angular momentum "about the axis". But the problem statement seems to be referring to an arbitrary system.

 

[lawsonfurther]

After you pointed out the confusion in the use of the word "axis", I start to realize that the origin and the frame of reference which is built on that origin are independent of the motion of the system, which means whatever the motion the system is in, once it is fixed, the velocity of any mass element of the system in any reference frame is unique.

Before that, I was thinking like the system may go through two different motions based on what rotation axis you choose. Yet this is not the case and that's why the question has not pointed out what motion the system is in.

It is good for you to point out the confusion in the use of "axis". The angular momentum of a system about a point should be the most appropriate statement in physics, in order not to cause any confusion. Now I understand it. Thank you so much. XD

 

[TSny]

OK. Glad it’s cleared up.