Angular Oscillation of a rod in a circle

[Tanya Sharma]

Homework Statement

A uniform rod moves in a vertical circle .Its ends are constrained to move on the track without friction.Find the angular frequency of small oscillation .

Homework Equations

The Attempt at a Solution

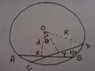
Suppose the rod of length L moves in a circle of radius R .
Let the equilibrium position of the rod be AB .X be the mid point .CD is the position of the rod when it displaced by an angle θ .Y is the mid point.

The mechanical energy of the rod in position CD is denoted by E .

The moment of inertia of the rod about its CM (the middle point) is I_cm
The moment of inertia of the rod about O is I .

I_{cm} = ML^2/12

I=I_{cm} + Md^2

I=M(R^2-\frac{L^2}{6})

E= mgd(1-cos\theta)+(1/2)I\dot\theta^2

Differentiating E w.r.t time ,we get

dE/dt = mgdsin\theta\dot\theta+(1/2)I(2\dot\theta\ddot\theta)

Since Mechanical energy remains conserved ,

Putting dE/dt=0 ,we get

\ddot\theta = -\frac{mgdsin\theta}{I}

Using small angle approximation , sinθ≈θ

\ddot\theta = -\frac{mgd\theta}{I}

Is my approach correct ?

 

[haruspex]

Looks right to me. (It's clearly the same as making a pendulum out of the rod by attaching a light bar length d rigidly, at right angles, to its centre.)