Inferior Mind
- 14
- 0
Calculate the tension in the cable connecting the two masses. Assume all surfaces are frictionless.
FBD
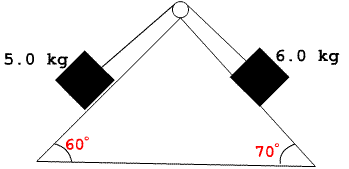
m1 = 5 kg
θ1 = 60°
m2 = 6 kg
θ2 = 70°
Equation 1 ~
FT - Fg = ma
FT - mgSinθ = ma
FT = 5a + 5(9.8)Sin60
FT = 5a + 42.44
Equation 2 ~
Fg - FT = ma
mgSinθ - FT = ma
6(9.8)Sin70 - 6a = FT
FT = 55.25 - 6a
~Set Equations Equal to Each Other ~
5a + 42.44 = 55.25 - 6a
11a = 12.81
a = 1.16 m/s2
~Sub into Eq to find Force Tension on da String Son !~
5(1.16) + 5(9.8)Sin60 = FT
FT = 48.2 N
FBD
m1 = 5 kg
θ1 = 60°
m2 = 6 kg
θ2 = 70°
Equation 1 ~
FT - Fg = ma
FT - mgSinθ = ma
FT = 5a + 5(9.8)Sin60
FT = 5a + 42.44
Equation 2 ~
Fg - FT = ma
mgSinθ - FT = ma
6(9.8)Sin70 - 6a = FT
FT = 55.25 - 6a
~Set Equations Equal to Each Other ~
5a + 42.44 = 55.25 - 6a
11a = 12.81
a = 1.16 m/s2
~Sub into Eq to find Force Tension on da String Son !~
5(1.16) + 5(9.8)Sin60 = FT
FT = 48.2 N