baby_1
- 159
- 16
Hello
how can we know with the definition of inverse function
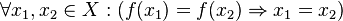
this function is inverse function or not?
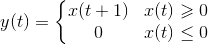 ?
?
another questions.
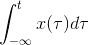
this function is inverse function because
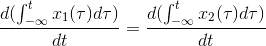
but if we have this function
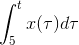
we can't do the same approach.why?(and it isn't a inverse function)
question 3:
in this function
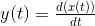
why we can't get Integral and say x1=x2?
how can we know with the definition of inverse function
this function is inverse function or not?
another questions.
this function is inverse function because
but if we have this function
we can't do the same approach.why?(and it isn't a inverse function)
question 3:
in this function
why we can't get Integral and say x1=x2?