- #1
FrogPad
- 810
- 0
I'm having difficulty visualizing what the output of an antenna looks like. Would someone care to explain?
This is where I am stuck. Imagine we have a point source that transmits energy. If at time t0 a pulse occurs which outputs a spherical wave, and some time later (say t1) another pulse occurs... From this I can see that we may define frequency, wavelength (say the wave travels at speed of light), etc...
Is this spherical wave made up of a bundle of cosine functions that propagate orthogonal to the wavefront? That is, do these cosine functions transmit outwards from the point source?
What does this diagram represent?
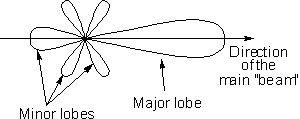
Is that the intensity of the cosine function given some spatial variable? So when we check the intensity in the "main" direction of the beam we may have, A(t)cos(O(t)) but if we angle off from the "main" direction we may have B(t)cos(O(t)) where A > B?Any help, or references to this would be highly appreciated.
This is where I am stuck. Imagine we have a point source that transmits energy. If at time t0 a pulse occurs which outputs a spherical wave, and some time later (say t1) another pulse occurs... From this I can see that we may define frequency, wavelength (say the wave travels at speed of light), etc...
Is this spherical wave made up of a bundle of cosine functions that propagate orthogonal to the wavefront? That is, do these cosine functions transmit outwards from the point source?
What does this diagram represent?
Is that the intensity of the cosine function given some spatial variable? So when we check the intensity in the "main" direction of the beam we may have, A(t)cos(O(t)) but if we angle off from the "main" direction we may have B(t)cos(O(t)) where A > B?Any help, or references to this would be highly appreciated.