Maestroo
- 2
- 0
I want to rotate an inclined plane to achieve a flat surface.
I think I can use the Euler angles to perform this operation.
Using following data:

and following rotation matrix
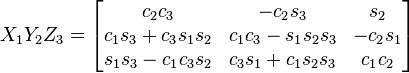
I think you can make the plane flat by following rotations:
1: rotation around x-axis by 45°
2: rotation around y-axis by -45°
3: no rotation around z-axis
filling in the rotation matrix:

new Z matrix derived from 3rd row: newZ=-X*cosd(45)*sind(-45)+Y*sind(45)+Z*cosd(45)*cosd(-45);
I expect a zero matrix, but this is not the case?
What am I doing wrong?
Thank you
I think I can use the Euler angles to perform this operation.
Using following data:

and following rotation matrix
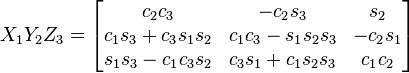
I think you can make the plane flat by following rotations:
1: rotation around x-axis by 45°
2: rotation around y-axis by -45°
3: no rotation around z-axis
filling in the rotation matrix:

new Z matrix derived from 3rd row: newZ=-X*cosd(45)*sind(-45)+Y*sind(45)+Z*cosd(45)*cosd(-45);
I expect a zero matrix, but this is not the case?
What am I doing wrong?
Thank you
