Pizzerer
- 10
- 0
Homework Statement
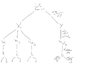
Write out a tree (this will be a big tree) of dependencies and hence write down an expression for
∂z/∂r
Homework Equations
z=k(x, y)=xy2, x=(w1)(w2)+w3, y=w4;
w1=t, w2=t2, w3=2t+1, w4=sin(t);
t=r2+2s2
The Attempt at a Solution
This is the tree I drew and followed the relevant paths in order to try and write and expression but my expression is to short. I only calculate 2 terms when there is suppose to be 8:
http://www.picpaste.com/Untitled_Image-OZCiTMvb.jpg
This is wrong however. I need 16 leaves at the base. What am I doing wrong?
Last edited by a moderator: