Approximating and regression method

[Iqbal94]

Hi guys,

I did a few sets of test in determining the natural frequency of a crane lifting loads. From that, I tried to find two constant from its initial function.

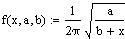
a is the stiffness of the pole that was holding the crane
b is the weight of the crane
x is the weight of the load

The tests were completed by using three different loads on three different position. I plotted the graph as below.

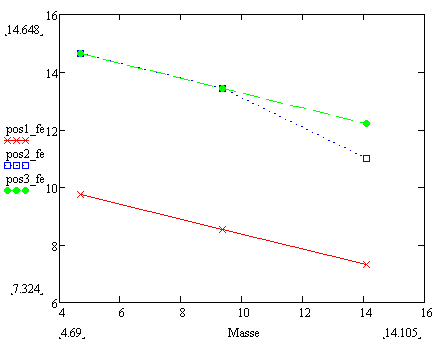
From the obtained graph and the initial function, I tried to determine the value of constant A and B. By calculating manually, the value of A and B are not constant but it supposed to be constant. I tried using MATHCAD to find the value of the constants by using nonlinear regression method but I am not convince that is a right solution. Any of you know any mathematical approximation method that I can use?

 

[Svein]

Any of you know any mathematical approximation method that I can use?

Excel does linear regression directly. If you want it mathematically, you must calculate:

1. s_{1}=\sum x_{j}
2. s_{2}=\sum x_{j}^{2}
3. t_{1}=\sum y_{j}
4. t_{2}=\sum y_{j}^{2}
5. v_{1}=\sum x_{j}\cdot y_{j}

Assuming that you have n points, you then calculate a=\frac{t_{1}\cdot s_{2}-s_{1}\cdot v_{1}}{n\cdot s_{2}-s_{1}^{2}} and b=\frac{n\cdot v_{1}-s_{1}\cdot t_{1}}{n\cdot s_{2}-s_{1}^{2}}. The regression line is then given by y=a\cdot x + b.