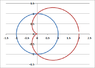
The discussion focuses on calculating the area inside the circle defined by the polar equation r=1 and outside the cardioid defined by r=1+cos(θ) using double integrals. Participants express confusion regarding the setup of the double integral, particularly in determining the correct limits for θ and r. The integration should be performed with r ranging from 1 to 1+cos(θ) and θ ranging from 0 to π, considering the symmetry of the regions involved. Visual aids, such as graphs, are recommended to clarify the intersection points and the areas of integration.
PREREQUISITESStudents studying calculus, particularly those focused on polar coordinates and double integrals, as well as educators looking for examples of area calculations involving complex shapes.
I did make a picture I am confused by the little piece of the cardoid that isn't in the first quadrant.BvU said:
stolencookie said:
As shown in BvU's graph, the region of integration is entirely on the left side of the vertical axis. What is ##\theta## at the upper intersection point? At the lower intersection point? There is also some symmetry you can take advantage of.stolencookie said:
Ambiguous -- in the picture a small piece is missing because I simply didn't grab the full ##\theta## range for the red curvestolencookie said:
