You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
MHB Area of Triangle ABC Given Dimensions
- Thread starter maxkor
- Start date
-
- Tags
- Area
AI Thread Summary
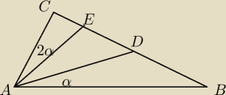
In triangle ABC, given the dimensions AC=BD, CE=2, ED=1, AE=4, and the angle relationship where angle CAE is twice angle DAB, the area of triangle ABC is being calculated. The discussion emphasizes the use of the law of cosines to find angles and side lengths, leading to the determination of angle alpha and the lengths AD and AB. There is a mention of using Geogebra for visual representation, but concerns are raised about the accuracy of the diagram. The calculations yield specific angle measures and side lengths, which are crucial for finding the area. The conversation highlights the importance of accurate diagrams and calculations in solving geometric problems.
Mathematics news on Phys.org
jonah1
- 107
- 0
Beer induced request follows.
We can't help you if we don't where you are stuck.
Please show us what you have tried and exactly where you are stuck.maxkor said:In triangle ABC $AC=BD, CE=2, ED=1, AE=4$ and $\angle CAE=2 \angle DAB$. Find area ABC.
We can't help you if we don't where you are stuck.
HOI
- 921
- 2
How did you get those?
maxkor
- 79
- 0
Geogebra...
mrtwhs
- 47
- 0
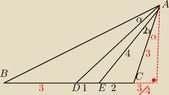
In your diagram, all three sides of $\triangle AEC$ are known. Using the law of cosines you get $2\alpha = \cos^{-1}(7/8)$ and $\alpha \approx 14.47751219^{\circ}$.
Continuing to use the law of cosines we get $AD=\dfrac{3\sqrt{10}}{2}$ and $AB=3\sqrt{6}$.
Finally, using the law of cosines on $\triangle ABD$ we get $\alpha \approx 71.170769^{\circ}$.
Your diagram is incorrect.
Continuing to use the law of cosines we get $AD=\dfrac{3\sqrt{10}}{2}$ and $AB=3\sqrt{6}$.
Finally, using the law of cosines on $\triangle ABD$ we get $\alpha \approx 71.170769^{\circ}$.
Your diagram is incorrect.
Hi,
I was watching the following video. I found some points confusing. Could you please help me to understand the gaps? Thanks, in advance!
Question 1:
Around 4:22, the video says the following.
So for those mathematicians, negative numbers didn't exist. You could subtract, that is find the difference between two positive quantities, but you couldn't have a negative answer or negative coefficients. Mathematicians were so averse to negative numbers that there was no single quadratic...
Insights auto threads is broken atm, so I'm manually creating these for new Insight articles.
In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra
Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/
by...
Here I made a terrible mistake of assuming this to be an equilateral triangle and set 2sinx=1 => x=pi/6. Although this did derive the double angle formulas it also led into a terrible mess trying to find all the combinations of sides. I must have been tired and just assumed 6x=180 and 2sinx=1. By that time, I was so mindset that I nearly scolded a person for even saying 90-x. I wonder if this is a case of biased observation that seeks to dis credit me like Jesus of Nazareth since in reality...
Similar threads
- Replies
- 4
- Views
- 1K
- Replies
- 3
- Views
- 2K
- Replies
- 4
- Views
- 1K
- Replies
- 1
- Views
- 1K
- Replies
- 2
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 1
- Views
- 1K
- Replies
- 1
- Views
- 1K
- Replies
- 2
- Views
- 1K
Hot Threads
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
-
B What could prove this wrong? I'm having a dispute with friends
- Started by ducknumerouno
- Replies: 94
- General Math
-
B About a definition: What is the number of terms of a polynomial P(x)?
- Started by littlemathquark
- Replies: 48
- General Math
-
B Geometry Puzzle with 20 points in a cross pattern
- Started by bob012345
- Replies: 31
- General Math
-
I Geometry problem of interest with a 3-4-5 triangle
- Started by Charles Link
- Replies: 59
- General Math
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 1
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math