- #1
karush
Gold Member
MHB
- 3,269
- 5
The coefficient of determination is 83.0 \%.
Provide an interpretation of this value.
$\begin{array}{rrrr}
x & y \\
12.17 & 1.88 \\
11.70 & 1.82 \\
11.63 & 1.77 \\
12.27 & 1.93 \\
12,03 & 1.83 \\
11.60 & 1.77 \\
12.15 & 1.83 \\
11.72 & 1.83 \\
11.30 & 1.70
\end{array}$
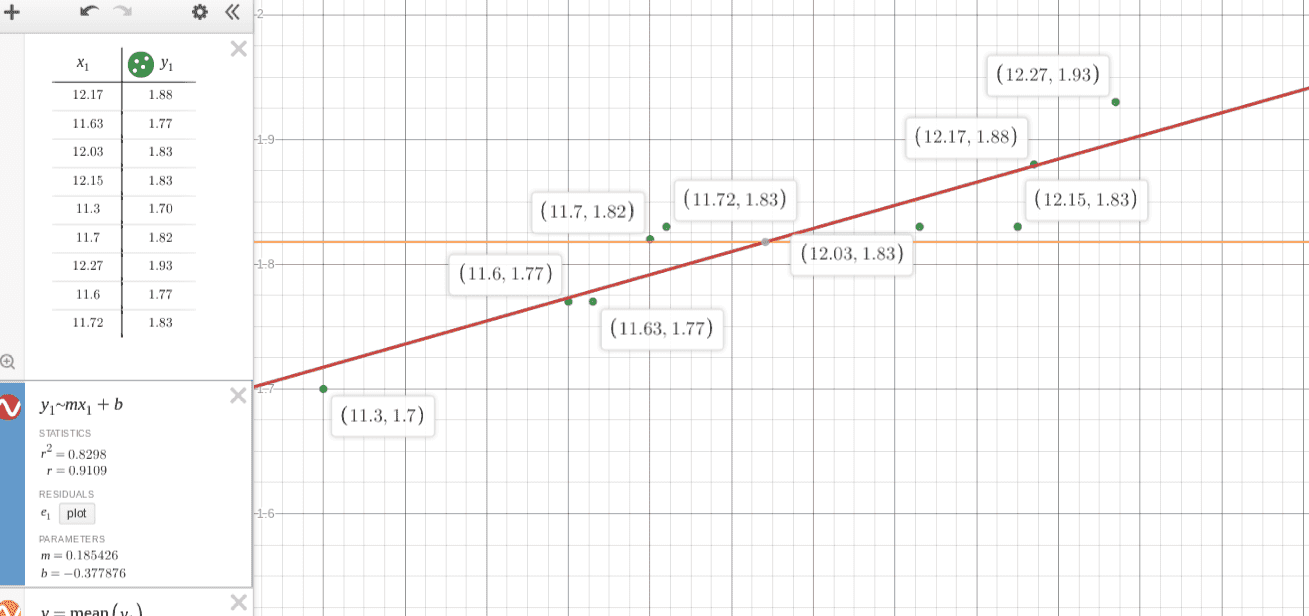
here is my desmos plot and I can see that R^2 is $83.0\%$
but after looking at some examples I don't see how it is derived
However, the interpretation of this is
of the variability in y is explained by the least-squares regression line.
Provide an interpretation of this value.
$\begin{array}{rrrr}
x & y \\
12.17 & 1.88 \\
11.70 & 1.82 \\
11.63 & 1.77 \\
12.27 & 1.93 \\
12,03 & 1.83 \\
11.60 & 1.77 \\
12.15 & 1.83 \\
11.72 & 1.83 \\
11.30 & 1.70
\end{array}$
here is my desmos plot and I can see that R^2 is $83.0\%$
but after looking at some examples I don't see how it is derived
However, the interpretation of this is
of the variability in y is explained by the least-squares regression line.
Last edited: