bardia sepehrnia
- 28
- 4
- Homework Statement
- Cooling water available at 10C is used to condense steam at 30C in the condenser of a power plant at a rate of 0.15kg/s by circulating the cooling water through a bank of 5-m-long 1.2cm-internal-diameter thin copper tubes. Water enters the tubes at a mean velocity of 4m/s, and leaves at a temperature of 24C. The tubes are nearly isothermal at 30 C. Determine the average heat transfer coefficient between the water and the tubes and the number of tubes needed to achieve the indicated heat transfer rate in the condenser.
- Relevant Equations
- Q=mcdeltaT, , Q=h*As*deltaTln, Re=(Vmean*Dh)/kinematic viscocity
Nu=0.023(Re^0.8)*(Pr^0.4), Nu=(h*Dh)/k
So firstly, I don't understand if the mass flow rate is for steam or for water. If it is for water, I know I can find the heat transfer rate using equation:Q=mcdeltaT.
But then I don't know how to find h (the average heat transfer coefficient) because I don't know the surface area (As). I can find the log mean temperature difference but there are still 2 unknowns in the equation: Q=h*As*deltaTln. Surface area and average heat transfer coefficient.
I also can calculate the Reynold number and ultimately calculate the Nusselt's number, but I still can't find out h because h=(Nu*Dh/k) which means h is function of diameter, and the diameter of 1 tube is known but since we don't know how many tubes is required, then the Dh is also unknown.
Any help will be appreciated.
My attempt with the solution and trying to use Nusselt number to find h.
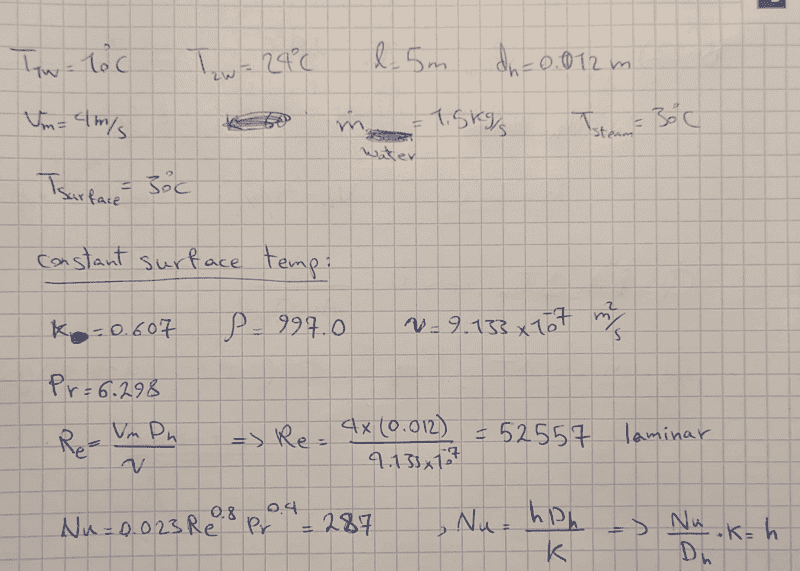
But then I don't know how to find h (the average heat transfer coefficient) because I don't know the surface area (As). I can find the log mean temperature difference but there are still 2 unknowns in the equation: Q=h*As*deltaTln. Surface area and average heat transfer coefficient.
I also can calculate the Reynold number and ultimately calculate the Nusselt's number, but I still can't find out h because h=(Nu*Dh/k) which means h is function of diameter, and the diameter of 1 tube is known but since we don't know how many tubes is required, then the Dh is also unknown.
Any help will be appreciated.
My attempt with the solution and trying to use Nusselt number to find h.