- #1
Terrell
- 317
- 26
So apparently the proof involves a trick that converts the problem of a general power set ##\mathscr{P}(M)## of some set ##M## which has of course the property of not having pairwise disjoint set-elements to a problem that involves disjoint set-elements. I do not understand why this trick is valid because I think by doing so, we are then "re-proving" the case where the set-elements are disjoint.
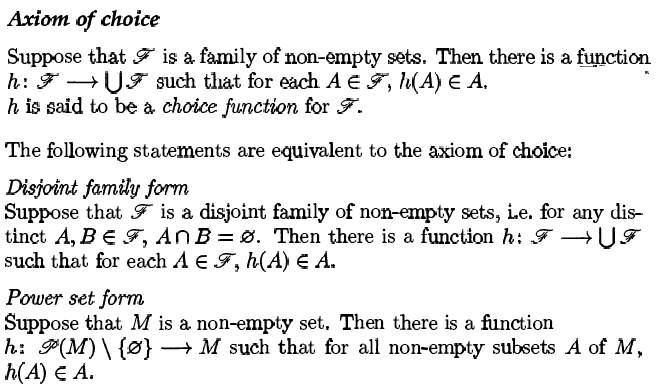

Attachments
Last edited:

