Bar suspended by rope kinetic energy

[rmfw]

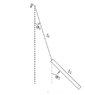
If I needed to calculate the kinetic energy of a bar suspended by a rope at one of its ends, in other words, a bar pendulum, do I need to calculate the kinetic energy of the center of mass plus the kinetic energy relatively to the center of mass or do I need to calculate the kinetic energy of the point located on the beginning of the bar (bar-rope junction) plus the kinetic energy relatively to that point? I'm thinking the first way is the right way, thanks.

Edit: Only the bar has mass, so when I speak of kinetic energy and center of mass I'm referring to the bar only.

 

[rmfw]

Also sorry for that doublepost, didn't meant to.

 

[Nugatory]

If I needed to calculate the kinetic energy of a bar suspended by a rope at one of its ends

Zero if the bar is not moving, but if that were the problem I don't suppose you'd be asking

And kidding aside, you'll have to tell us more about the problem (which, depending on little details like whether the rope is "ideal" or not, may be seriously hairy) and especially the motion that the bar is undergoing.

At any given moment the kinetic energy of the bar is the sum of the translational kinetic energy $\frac{mv^2}{2}$ calculated at the centter of mass of the bar and the rotational kinetic energy $I\omega^2$. However, these will change in possibly non-trivial ways as the rope jerks the bar around.

 

[rmfw]

I have added a picture to the original post.

Ok so $T = \frac{ m v_{centerofmass}^2}{2} + \frac{I w^2}{2}$

So now I still don't know if I should use $I = \frac {m L^2}{12}$ (rotation about the center of mass) or $I = \frac {m L^2}{3}$ (rotation at the beginning of the bar)

 

[rmfw]

Ok I already know the answer is $I = \frac{m L ^2}{12}$ . But there's something else bothering me, if there were no rope, only the bar fixed at its beginning (origin) and oscillating in a 2D plane, then the kinetic energy would be only in rotational motion calculated using $I = \frac{m L ^2}{3}$ , what differs from one case to the other? In this second example the center of mass is also moving and there's also rotation relatively to the center of mass. This is really confusing me.

 

[dauto]

You're doing a pretty good job at answering your own questions. Just keep going. Kidding aside, Kidding aside, The total kinetic energy is given by the tanslational energy (using the speed of the center of mass) plus the rotational energy around the center of mass.

 

[rmfw]

Ok I understood that, but my question still remains, (see pic attached in this post) in this case, I know the answer for kinetic energy is $T = \frac{1}{2} \dot{\theta}^2 \frac{m L^2}{3} = \dot{\theta}^2 \frac{m L^2}{6}$

But, according to this statement "The total kinetic energy is given by the tanslational energy (using the speed of the center of mass) plus the rotational energy around the center of mass. "

Why isn't it $T= \frac{m V_{cm}^2}{2} + \frac{1}{2} \dot{\theta}^2 \frac{m L^2}{12} = \frac{m (\frac{L}{2} \dot{\theta})^2}{2} + \frac{1}{2} \dot{\theta}^2 \frac{m L^2}{12}= 4 \dot{\theta}^2 \frac{m L^2}{24} = \dot{\theta}^2 \frac{m L^2}{6}$

Dear lord, what kind of sorcery is this? I should have checked the results before even asking it. Thanks anyway, I get it now